四头牛被拴在一个边长为50米的正方形地块的四个角上，它们刚好够不着彼此。请问有多少面积没有被放牧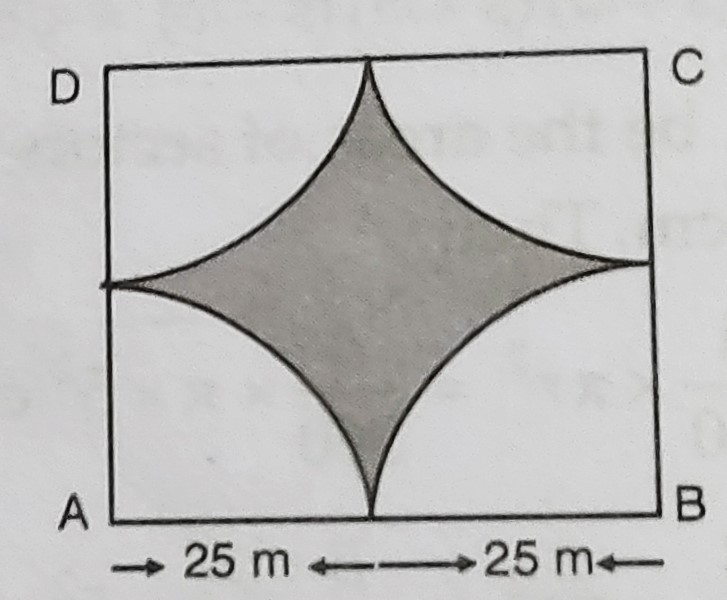？"\n

已知

四头牛被拴在一个边长为50米的正方形地块的四个角上，它们刚好够不着彼此。

要求

我们需要求出未被放牧的面积。

解答

根据图形，

正方形边长 $= 50\ 米$

这意味着，

每个象限的半径 $r = \frac{50}{2}$

$=25\ 米$

因此，

正方形田地的面积 $= (50)^2\ 米^2$

$= 2500\ 米^2$

每个象限的面积 $=\frac{1}{4} \pi r^{2}$

四个象限的总面积 $=4\times\frac{1}{4} \pi r^{2}$

$=\pi r^{2}$

$=\frac{22}{7} \times(25)^{2}$

$=\frac{22}{7} \times 625$

$=1964.29 \mathrm{~米}^{2}$
未放牧的面积 $=$ 正方形田地的面积 $-$ 四个象限的总面积

$=2500-1964.29$

$=2500 - 1964.29 = 535.71 \mathrm{~米}^{2}$

未被放牧的面积是 $535.71 \mathrm{~米}^{2}$。

教程点

更新于: 2022年10月10日

浏览量：179

启动您的职业生涯

完成课程获得认证

开始学习