数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律列出下列两个数之间五个有理数
(i) $-1$ 和 $0$
(ii) $-2$ 和 $-1$
已知
给定的数字是
(i) $-1$ 和 $0$ (ii) $-2$ 和 $-1$
要求
我们必须列出给定数字之间的五个有理数。
解答
(i) $-1$ 和 $0$ 之间的五个有理数
我们可以将 $-1, 0$ 写成 $\frac{-6}{6}, \frac{0}{6}$
所以 $\frac{-6}{6}$ 和 $\frac{0}{6}$ 之间的 5 个有理数是
$\frac{-5}{6}, \frac{-4}{6}, \frac{-3}{6}, \frac{-2}{6}, \frac{-1}{6}$。
(ii) $-2$ 和 $-1$ 之间的五个有理数。要在 $-2$ 和 $-1$ 之间绘制 5 个有理数，将 $-2$ 和 $-1$ 之间的线段分成至少 6 部分。
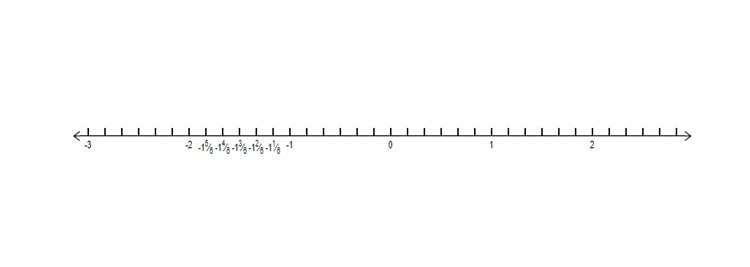
为方便起见，将其分成 6 等份。
由于线段的总长度为 1 个单位，因此每部分的长度为 $\frac{1}{6}$ 个单位。
所以，第一个点是 $-2 +\frac{1}{6}$，即 $\frac{-11}{6} = -1\frac{5}{6}$
同样地，
接下来的 4 个有理数是：
$-2 + \frac{2}{6} =\frac{-12 + 2}{6} = \frac{-10}{6} = -1 \frac{4}{6}$。
$-2 + \frac{3}{6} =\frac{-12 + 3}{6} = \frac{-9}{6} = -1 \frac{3}{6}$。
$-2 + \frac{4}{6} =\frac{-12 + 4}{6} = \frac{-8}{6} = -1 \frac{2}{6}$。
$-2 + \frac{5}{6} =\frac{-12 + 5}{6} = \frac{-7}{6} = -1 \frac{1}{6}$。
因此，$-1$ 和 $-2$ 之间的五个有理数是 $-1\frac{5}{6}, -1\frac{4}{6}, -1\frac{3}{6}, -1\frac{2}{6}, -1\frac{1}{6}$。
63 次浏览
