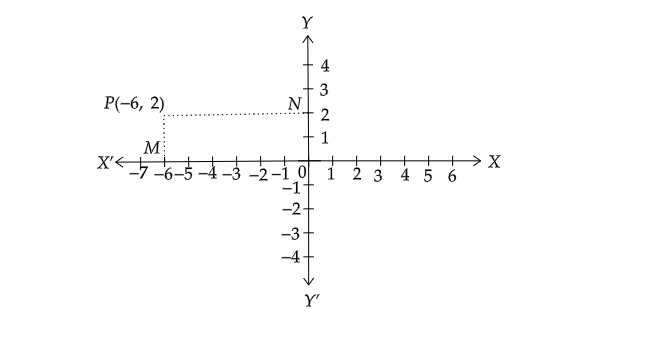
绘制点$P( -6,\ 2)$，并从该点分别作$PM$和$PN$垂直于$x$轴和$y$轴。写出点$M$和$N$的坐标。

已知：点$P( -6,\ 2)$。

要求：绘制该点。分别作$PM$和$PN$垂直于$x$轴和$y$轴。写出点$M$和$N$的坐标。

解答



i). 绘制点$P( -6,\ 2)$。

ii). 点$P( -6,\ 2)$位于第二象限。

iii). 分别作$PM$和$PN$垂直于$x$轴和$y$轴。

因为$x$轴上$y$坐标始终为$0$。

因此，点$M$的坐标为$( -6,\ 0)$

类似地，$y$轴上$x$坐标始终为$0$。

因此，点$N$的坐标为$( 0,\ 2)$。
 

更新于： 2022年10月10日

58 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习
广告