证明圆周角大于半圆的角小于直角。

待办事项

我们必须证明圆周角大于半圆的角小于直角。

解答

设在以O为圆心的圆中，大于半圆的弓形ACB内接有∠ACB。

连接OA和OB。

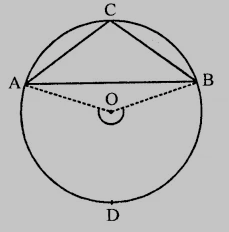
弧ADB在圆心处构成∠AOB，在圆周其余部分构成∠ACB。

因此，

∠ACB = ½∠AOB

∠AOB < 180°

这意味着，

∠ACB < 90°

∠ACB < 90°

因此∠ACB < 90°

教程点

更新于：2022年10月10日

67 次浏览

开启你的职业生涯

完成课程获得认证

开始学习