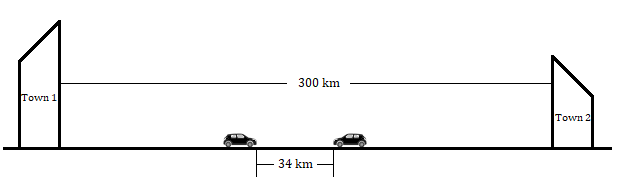
两个城镇之间的距离是 300 公里。两辆汽车同时从这两个城镇出发，相向行驶。一辆汽车的速度比另一辆快 7 公里/小时。如果两辆汽车 2 小时后的距离是 34 公里，求这两辆汽车的速度。

已知：

两个城镇之间的距离 = 300 公里

一辆汽车的速度比另一辆快 7 公里/小时

两辆汽车 2 小时后的距离是 34 公里

求解：我们需要求出这两辆汽车的速度。

解

设从城镇 1 出发的汽车为汽车 A，从城镇 2 出发的汽车为汽车 B。

设汽车 A 的速度为 $x$ 公里/小时

因此，汽车 B 的速度为 $(x\ +\ 7)$ 公里/小时

我们知道

距离 = 速度 $\times$ 时间

现在，两辆汽车 2 小时后的距离是 34 公里;

汽车 A 在 2 小时内行驶的距离 = $2x$ 公里

汽车 B 在 2 小时内行驶的距离 = $2(x\ +\ 7)$ = $(2x\ +\ 14)$ 公里

两辆汽车 2 小时后的距离 = 总距离 $-$ 汽车 A 行驶的距离 $-$ 汽车 B 行驶的距离

$34\ =\ 300\ -\ 2x\ -\ (2x\ +\ 14)$

$34\ =\ 300\ -\ 4x\ -\ 14$

$34\ =\ 286\ -\ 4x$

$4x\ =\ 286\ -\ 34$

$4x\ =\ 252$

$x\ =\ \frac{252}{4}$

$x\ =\ 63$

因此，

汽车 A 的速度 = $x$ = 63 公里/小时

汽车 B 的速度 = $(x\ +\ 7)$ = $63\ +\ 7$ = 70 公里/小时

所以，汽车的速度分别为 63 公里/小时和 70 公里/小时。

教程点

更新于： 2022 年 10 月 10 日

271 次查看

开启您的 职业生涯

通过完成课程获得认证

开始学习