下表显示了一个班级 30 名学生的体重分布。求学生体重的中位数

体重（公斤）	40-45	45-50	50-55	55-60	60-65	65-70	70-75
学生人数	2	3	8	6	6	3	2

已知

该分布显示了一个班级 30 名学生的体重。

要求

我们需要求学生体重的中位数。

解答

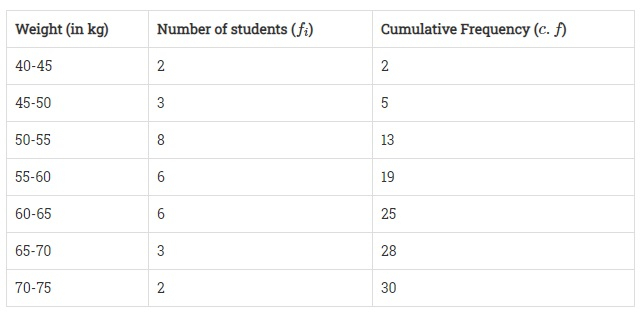
这里，

$N = 30$

$\frac{N}{2} = \frac{30}{2} = 15$

累积频率刚好大于 $\frac{N}{2}$ 的值为 19，对应的组为 55 – 60。

这意味着，55– 60 是中位数组。

因此，

$l = 55, f = 6, F = 13$ 且 $h = (60 - 55) = 5$

中位数 $=\mathrm{l}+\frac{\frac{\mathrm{N}}{2}-\mathrm{F}}{\mathrm{f}} \times \mathrm{h}$

$=55+\frac{15-13}{6} \times 5$

$=55+\frac{2}{6} \times 5$

$=55+\frac{5}{3}$

$= 55 + 1.67$

$= 56.67$

学生体重的中位数为 56.67 公斤。 

教程点

更新时间： 2022 年 10 月 10 日

72 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习