三角形的中位线和质心是什么

中位线

中位线是指连接顶点和对边中点的线段。中位线可以垂直也可以非垂直，具体取决于三角形的类型。

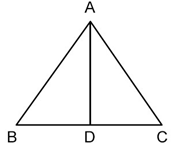
在以下三角形 ABC 中，AD 是中位线，连接顶点 A 和 BC 的中点 D。

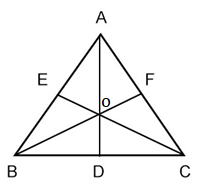
三角形的质心是三角形三条中位线的交点。在下面的三角形中，AD、BF 和 CE 是中位线，点 O 是圆的质心。

Tutorialspoint

更新于：2022-10-10

48 次浏览

开启你的 职业生涯

完成课程后获得认证

开始学习