质心

---

引言

在数学中，质心指的是二维平面图形的几何中心。在本教程中，我们将学习质心以及三角形的其他中心及其之间的关系。

什么是质心？

在数学中，质心指的是二维平面图形的几何中心。它是通过取平面图形上所有点的算术平均值来确定其位置的点。“质心”一词也指重心。

确定三角形的质心 - 三角形的三条中线相交的点称为质心。三角形的中线是一条连接顶点与其对面中点的线段。

对于三角形 ABC，具有 AA₁、BB₁ 和 CC₁ 作为中线，用 p 表示的质心如下所示。

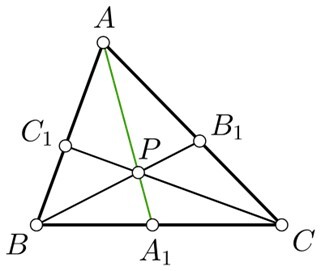
三角形的其他中心

除了质心之外，三角形还有三种类型的中心，即垂心、内心和外心。

• 垂心 - 从三角形的顶点垂直于其对边作垂线，其交点称为垂心。

  垂心可能位于三角形内部或外部，这取决于三角形的类型。

在上图中，三条垂线的交点是垂心。

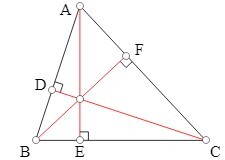
• 内心 - 三角形的三条内角平分线的交点构成三角形的内心。

  内接于三角形的三角形内切圆的圆心也称为三角形的内心。

在上图中，三条内角平分线的交点是内心，用 I 表示。

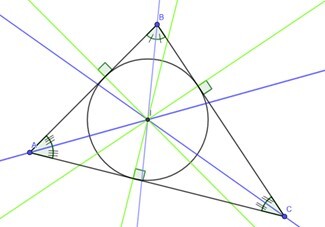
• 外心 - 三角形的外心可以作为三角形所有边的垂直平分线的交点求出。

  三角形的每个顶点到外心的距离都相等。

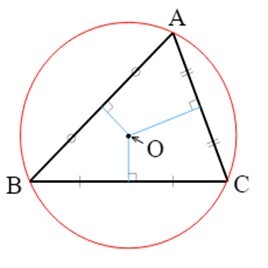
在上图中，三条垂直平分线的交点是外心，用 O 表示。

质心的性质

• 质心是物体的几何中心。

• 平面图形中所有点的算术平均位置称为图形的质心或几何中心。

• 三角形的质心始终位于三角形内，因为中线位于三角形内。

• 可以通过对三角形三条边的 x 和 y 坐标取平均值来确定质心。

• 质心是三角形中最常见的并发点。其在数学和物理学中的重要性源于它是三角形的几何中心。

• 质心将中线分成 2:1 的比例。

  • 最长线段最靠近顶点，质心将每条中线分成长度为 2:1 的两条线段。

• 质心定理：三角形的质心位于从顶点到边的中点的距离的 2/3 处。

  • 对于三角形 ABC，具有 A¹、B¹ 和 C¹ 作为中线，质心 p

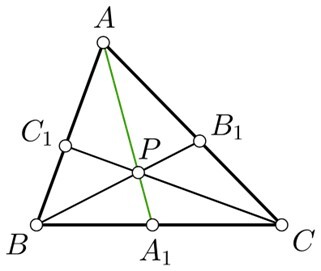
• 这里使用质心定理，$\mathrm{AP=\frac{2}{3} AA_1}$

• 类似地，$\mathrm{BP=\frac{2}{3} BB_1\:and\: CP=\frac{2}{3} CC_1}$

三角形质心的坐标

可以通过取三角形顶点的平均值来计算质心的坐标。

对于三角形 ABC，具有 A¹、B¹ 和 C¹ 作为中线，并且设 A 顶点的坐标为 (x¹,y¹)，B 顶点的坐标为 (x²,y²)，C 顶点的坐标为 (x³,y³)，则

质心的坐标为 $C=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3}).$

质心坐标的推导

在上图三角形 ABC 中，设 A 顶点的坐标为 (x¹,y¹)，A 顶点的坐标为 (x²,y²)，C 顶点的坐标为 (x³,y³)

这里三角形的中点分别是 BC、AC 和 AB 的 A¹、B¹ 和 C¹，我们知道中线将三角形的边分成两等分。

现在通过应用中点公式对于 A¹，A¹ 的坐标将是，$\mathrm{(\frac{x_2+x_3}{2},\frac{y_2+y_3}{2})}$

现在根据质心的性质，如上所述，质心将中线分成 2:1 的比例，因此我们可以使用截面公式。

设 P 为三角形 ABC 的质心，

$$\mathrm{P=(\frac{\frac{2(x_2+x_3)}{2}+1(x_1)}{2+1},\frac{\frac{2(y_2+y_3)}{2}+1(y_3)}{2+1})}$$

简化后，

$$\mathrm{P=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})}$$

等边三角形

等边三角形是三条边长度相等的三条边。等边三角形的质心位于三角形的中心。

从每个三角形顶点到对边画垂直线，以获得质心。质心是所有这些垂直线（长度都相等）相交的地方。

等边三角形的中线、角平分线和高线都相同。因此，等边三角形的所有中心都相同。

可以计算质心到等边三角形任何顶点的距离 -

设 a 为等边三角形中任何一边的长度，根据等边三角形的性质，我们知道等边三角形的高度为：

$$\mathrm{h=\frac{√3}{2} a}$$

根据质心的性质，我们知道质心将中线分成 2:1 的比例。

因此，等边三角形质心到其任何顶点的距离

= 等边三角形高度的 2/3 =$\mathrm{\frac{2}{3}×\frac{√3}{2} a}$

$$\mathrm{=\frac{a}{√3}.}$$

例题

1) 求坐标为 P(15,4)、Q(4,-6)、R(5,12) 的三角形的质心

求质心坐标的公式为，$\mathrm{C=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})}$

因此，这里我们有 x_1=15，x_2=4，x_3=5 和 y_1=4，y_2=-6，y_3=12

将这些值代入上述 C 的公式，我们有

$$\mathrm{C=(\frac{15+4+5}{3},\frac{4-6+12}{3})=(\frac{24}{3},\frac{10}{3})}$$

因此，质心的坐标为，$\mathrm{(8,\frac{10}{3})}$.

2) 求坐标为 A(-3,3)、B(3,1)、C(-1,-1) 的三角形的质心

求质心坐标的公式为，$\mathrm{C=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})}$

因此，这里我们有 x₁=-3，x₂=3，x₃=-1 和 y₁=3，y₂=1，y₃=-1

将这些值代入上述 C 的公式，我们有

$$\mathrm{C=(\frac{-3+3-1}{3},\frac{3+1-1}{3})=(\frac{-1}{3},\frac{3}{3})}$$

因此，质心的坐标为，$\mathrm{(\frac{-1}{3},1).}$

结论

在数学中，质心指的是二维平面图形的几何中心。三角形的三个中线相交产生三角形的质心。它是三角形的四个并发点之一。角平分线的交点位于内心。而中线的交点称为质心。虽然质心将其中线分成 2:1 的比例，但内心并不特别划分角平分线。内心和质心都位于三角形内部。

常见问题

1. 什么是三角形的质心？

三角形的三个中线相交产生三角形的质心。它是三角形的四个并发点之一。质心实际上是三角形的几何中心。

2. 什么是质心定理？

质心定理指出，三角形的质心位于从顶点到边的中点的距离的 2/3 处。

3. 质心和内心有什么区别？

角平分线的交点位于内心。而中线的交点称为质心。虽然质心将其中线分成 2:1 的比例，但内心并不特别划分角平分线。内心和质心都位于三角形内部。

4. 质心和垂心有什么区别？

垂线的交点位于垂心。而中线的交点称为质心，虽然质心将其中线分成 2:1 的比例，但垂心并不特别划分角平分线。垂心位于三角形外部，而质心位于三角形内部。

5. 计算质心的公式是什么？

可以通过取三角形顶点的平均值来计算质心的坐标。对于三角形 ABC，设 A 顶点的坐标为 (x₁,y₁)，B 顶点的坐标为 (x₂,y₂)，C 顶点的坐标为 (x₃,y₃)，则质心的坐标为

$$\mathrm{C=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3}).}$$