
雷达系统 - 延迟线抵消器
本章将学习雷达系统中的延迟线抵消器。顾名思义,延迟线引入一定的延迟。因此,延迟线主要用于延迟线抵消器,以引入脉冲重复时间的延迟。
延迟线抵消器是一种滤波器,它消除来自静止目标的回波信号的直流分量。这意味着它允许来自非静止目标(即移动目标)的回波信号的交流分量通过。
延迟线抵消器的类型
根据延迟线数量的不同,延迟线抵消器可以分为以下两种类型。
- 单延迟线抵消器
- 双延迟线抵消器
在接下来的章节中,我们将更详细地讨论这两种延迟线抵消器。
单延迟线抵消器
延迟线和减法器的组合称为延迟线抵消器。它也称为单延迟线抵消器。带单延迟线抵消器的MTI接收机的框图如下所示。(此处应插入图片)
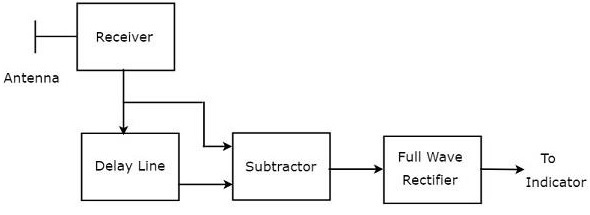
我们可以写出多普勒效应后接收到的回波信号的数学方程为:
$$V_1=A\sin\left [ 2\pi f_dt-\phi_0 \right ]\:\:\:\:\:公式\:1$$
其中:
A 是视频信号的幅度
$f_d$ 是多普勒频率
$\phi_o$ 是相移,等于 $4\pi f_tR_o/C$
通过在公式1中用 $t-T_P$ 代替 $t$,我们将得到延迟线抵消器的输出。
$$V_2=A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]\:\:\:\:\:公式\:2$$
其中:
$T_P$ 是脉冲重复时间
通过从公式1中减去公式2,我们将得到减法器的输出。
$$V_1-V_2=A\sin\left [ 2\pi f_dt-\phi_0 \right ]-A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]$$
$$ \Rightarrow V_1-V_2=2A\sin\left [ \frac{ 2\pi f_dt-\phi_0-\left [ 2\pi f_d\left ( t-T_P \right )-\phi_0 \right ]}{2}\right ]\cos\left [ \frac{ 2\pi f_dt-\phi_o+2\pi f_d\left ( t-T_P \right )-\phi_0 }{2}\right ]$$
$$V_1-V_2=2A\sin\left [ \frac{2\pi f_dT_P}{2} \right ]\cos\left [ \frac{2\pi f_d\left ( 2t-T_P \right )-2\phi_0}{2} \right ]$$
$$ \Rightarrow V_1-V_2=2A\sin\left [ \pi f_dT_p \right ]\cos\left [ 2\pi f_d\left ( t-\frac{T_P}{2} \right )-\phi_0 \right ]\:\:\:\:\:公式\:3$$
减法器的输出作为输入应用于全波整流器。因此,全波整流器的输出如下所示。(此处应插入图片)它只不过是单延迟线抵消器的频率响应。
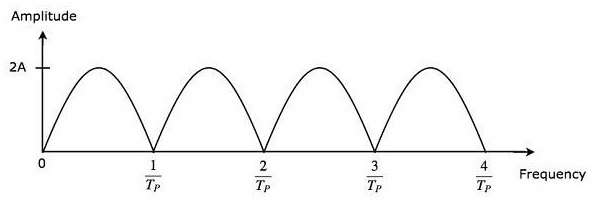
从公式3可以看出,当 $\pi f_dT_P$ 等于π 的整数倍时,单延迟线抵消器的频率响应变为零。这意味着 $\pi f_dT_P$ 等于 $n\pi$。数学上,可以写成:
$$ \pi f_dT_P=n\pi$$
$$ \Rightarrow f_dT_P=n$$
$$ \Rightarrow f_d=\frac{n}{T_P}\:\:\:\:\:公式\:4$$
从公式4可以得出结论,当多普勒频率 $f_d$ 等于脉冲重复时间 $T_P$ 倒数的整数倍时,单延迟线抵消器的频率响应变为零。
我们知道脉冲重复时间和脉冲重复频率之间的以下关系。
$$f_d=\frac{1}{T_P}$$
$$ \Rightarrow \frac{1}{T_P}=f_P\:\:\:\:\:公式\:5$$
将公式5代入公式4,我们将得到以下公式。
$$ \Rightarrow f_d=nf_P\:\:\:\:\:公式\:6$$
从公式6可以得出结论,当多普勒频率 $f_d$ 等于脉冲重复频率 $f_P$ 的整数倍时,单延迟线抵消器的频率响应变为零。
盲速
从我们目前所学,当 $n$ 等于零时,单延迟线抵消器消除来自静止目标的回波信号的直流分量。除此之外,当多普勒频率 $f_d$ 等于脉冲重复频率 $f_P$ 的整数(非零)倍时,它还会消除来自非静止目标的回波信号的交流分量。
因此,单延迟线抵消器的频率响应变为零的相对速度称为盲速。数学上,我们可以将盲速 $v_n$ 的表达式写为:
$$v_n=\frac{n\lambda}{2T_P}\:\:\:\:\:公式\:7$$
$$ \Rightarrow v_n=\frac{n\lambda f_P}{2}\:\:\:\:\:公式\:8$$
其中:
$n$ 是整数,等于 1、2、3 等
$\lambda$ 是工作波长
例题
一台MTI雷达工作频率为$6GHZ$,脉冲重复频率为$1KHZ$。求该雷达的一、二、三盲速。
解答
已知:
MTI雷达的工作频率,$f=6GHZ$
脉冲重复频率,$f_P=1KHZ$。
以下是根据工作频率 f 计算工作波长 $\lambda$ 的公式。
$$ \lambda=\frac{C}{f}$$
在上述公式中代入 $C=3\times10^8m/sec$ 和 $f=6GHZ$。
$$ \lambda=\frac{3\times10^8}{6\times10^9}$$
$$ \Rightarrow \lambda=0.05m$$
因此,当工作频率 f 为 $6GHZ$ 时,工作波长 $\lambda$ 等于 $0.05m$。
我们知道盲速公式如下:
$$v_n=\frac{n\lambda f_p}{2}$$
在上述公式中代入 $n$=1,2 & 3,我们将分别得到一、二、三盲速的以下公式。
$$v_1=\frac{1\times \lambda f_p}{2}=\frac{\lambda f_p}{2}$$
$$v_2=\frac{2\times \lambda f_p}{2}=2\left ( \frac{\lambda f_p}{2} \right )=2v_1$$
$$v_3=\frac{3\times \lambda f_p}{2}=3\left ( \frac{\lambda f_p}{2} \right )=3v_1$$
在第一盲速公式中代入 $\lambda$ 和 $f_P$ 的值。
$$v_1=\frac{0.05\times 10^3}{2}$$
$$ \Rightarrow v_1=25m/sec$$
因此,对于给定的规格,第一盲速 $v_1$ 等于 $25m/sec$。
通过在第二和第三盲速公式中代入 𝑣1 的值,我们将分别得到第二和第三盲速的值为 $50m/sec$ 和 $75m/sec$。
双延迟线抵消器
我们知道单延迟线抵消器由延迟线和减法器组成。如果将两个这样的延迟线抵消器级联在一起,则该组合称为双延迟线抵消器。双延迟线抵消器的框图如下所示。(此处应插入图片)

设 $p\left ( t \right )$ 和 $q\left ( t \right )$ 分别为第一个延迟线抵消器的输入和输出。我们将从第一个延迟线抵消器得到以下数学关系。
$$q\left ( t \right )=p\left ( t \right )-p\left ( t-T_P \right )\:\:\:\:\:公式\:9$$
第一个延迟线抵消器的输出作为输入应用于第二个延迟线抵消器。因此,$q\left ( t \right )$ 将成为第二个延迟线抵消器的输入。设 $r\left ( t \right )$ 为第二个延迟线抵消器的输出。我们将从第二个延迟线抵消器得到以下数学关系。
$$r\left ( t \right )=q\left ( t \right )-q\left ( t-T_P \right )\:\:\:\:\:公式\:10$$
在公式9中将 $t$ 替换为 $t-T_P$。
$$q\left ( t-T_P \right )=p\left ( t-T_P \right )-p\left ( t-T_P-T_P \right )$$
$$q\left ( t-T_P \right )=p\left ( t-T_P \right )-p\left ( t-2T_P \right )\:\:\:\:\:公式\:11$$
在公式10中代入公式9和公式11。
$$r\left ( t \right )=p\left ( t \right )-p\left ( t-T_P \right )-\left [ p\left ( t-T_P \right )-p\left ( t-2T_P \right ) \right ]$$
$$ \Rightarrow r\left ( t \right )=p\left ( t \right )-2p\left ( t-T_P \right )+p\left ( t-2T_P \right )\:\:\:\:\:公式\:12$$
双延迟线抵消器的优点是它可以广泛地抑制杂波。两个级联的延迟线抵消器的输出将等于单个延迟线抵消器输出的平方。
因此,存在于MTI雷达接收器中的双延迟线抵消器的输出幅度将等于 $4A^2\left ( \sin\left [ \pi f_dT_P \right ] \right )^2$。
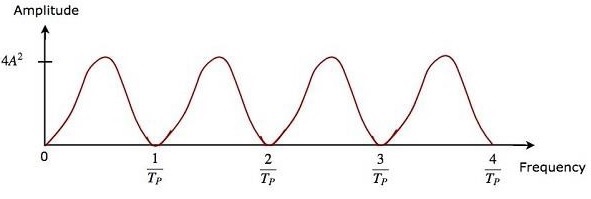
双延迟线抵消器和两个延迟线抵消器级联组合的频率响应特性相同。时域延迟线抵消器的优点是它可以在所有频率范围内工作。