雷达系统 - 匹配滤波器接收机

如果滤波器的输出以最大化其频率响应中输出峰值功率与平均噪声功率之比的方式产生，则该滤波器称为匹配滤波器。

这是一个重要的标准，在设计任何雷达接收机时都会考虑。在本章中，让我们讨论匹配滤波器的频率响应函数和匹配滤波器的冲激响应。

匹配滤波器的频率响应函数

匹配滤波器的频率响应将与输入信号频谱的复共轭成正比。数学上，我们可以将匹配滤波器的频率响应函数 $H\left (f\right )$ 表示为：

$$H\left (f\right )=G_aS^\ast\left (f\right )e^{-j2\pi ft_1}\:\:\:\:\:公式\:1$$

其中：

$G_a$ 是匹配滤波器的最大增益

$S\left (f\right )$ 是输入信号 $s\left (t\right )$ 的傅里叶变换

$S^\ast\left (f\right )$ 是 $S\left (f\right )$ 的复共轭

$t_1$ 是观察到信号最大的时刻

一般情况下，$G_a$ 的值取为1。将 $G_a=1$ 代入公式1，我们将得到以下公式：

$$H\left (f\right )=S^\ast\left (f\right )e^{-j2\pi ft_1}\:\:\:\:\:公式\:2$$

匹配滤波器的频率响应函数 $H\left (f\right )$ 的幅度为 $S^\ast\left (f\right )$，相位角为 $e^{-j2\pi ft_1}$，它随频率均匀变化。

匹配滤波器的冲激响应

在时域中，我们将通过对频率响应函数 $H(f)$ 进行傅里叶逆变换得到匹配滤波器接收机的输出 $h(t)$。

$$h\left (t\right )=\int_{-\infty }^{\infty }H\left (f\right )e^{-j2\pi ft_1}df\:\:\:\:\:公式\:3$$

将公式1代入公式3。

$$h\left (t\right )=\int_{-\infty }^{\infty }\lbrace G_aS^\ast\left (f\right )e^{-j2\pi ft_1}\rbrace e^{j2\pi ft}df$$

$$\Rightarrow h\left (t\right )=\int_{-\infty }^{\infty }G_aS^\ast\left (f\right )e^{-j2\pi f\left (t_1-t\right )}df\:\:\:\:\:公式\:4$$

我们知道以下关系。

$$S^\ast\left (f\right )=S\left (-f\right )\:\:\:\:\:公式\:5$$

将公式5代入公式4。

$$h\left (t\right )=\int_{-\infty }^{\infty }G_aS(-f)e^{-j2\pi f\left (t_1-t\right )}df$$

$$\Rightarrow h\left (t\right )=\int_{-\infty }^{\infty }G_aS^\left (f\right )e^{j2\pi f\left (t_1-t\right )}df$$

$$\Rightarrow h\left (t\right )=G_as(t_1−t)\:\:\:\:\:公式\:6$$

一般情况下，$G_a$ 的值取为1。将 $G_a=1$ 代入公式6，我们将得到以下公式：

$$h(t)=s\left (t_1-t\right )$$

上述公式证明了匹配滤波器的冲激响应是接收信号关于时刻 $t_1$ 的镜像。下图说明了这个概念。

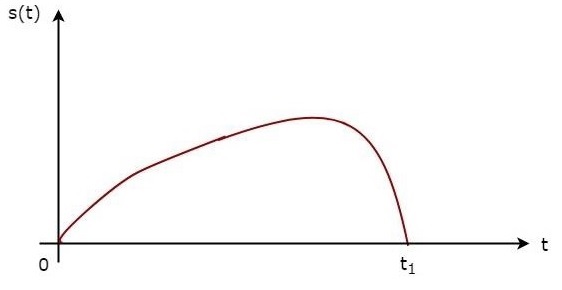
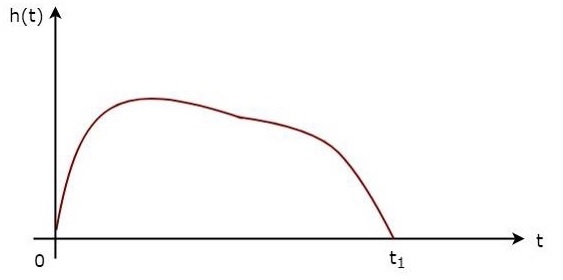
上图显示了接收信号 $s\left (t\right )$ 和与信号 $s\left (t\right )$ 相对应的匹配滤波器的冲激响应 $h\left (t\right )$。