直角三角形：作图 (RHS)

---

引言

三角学这个词的意思是三角测量，也就是三个角的测量。当我们取任何多边形，例如正方形、矩形、五边形、六边形等时，我们可以将每个多边形分成三角形。所以三角学主要处理三角形。根据角度测量，三角形有三种类型。它们是锐角三角形、钝角三角形和直角三角形。

锐角三角形−三个内角的度数都小于90°。

钝角三角形−三个内角的度数都大于90°。

直角三角形−至少一个内角的度数为90°。

直角三角形

在三角学中，直角三角形比其他两种三角形更重要。我们可以将锐角三角形和钝角三角形分成直角三角形。直角三角形有三条边和三个角。

角分别是$\mathrm{\angle\:ABC\:,\:\angle\:BCA\:,\:\angle\:CAB}$，边分别是AB、BC、CA

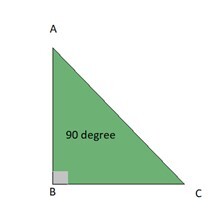
在直角三角形中，勾股定理在求解缺失边的长度时起着重要的作用。

$\mathrm{AC^{2}\:=\:AB^{2}\:+\:BC^{2}}$

其中AC是斜边。

三角形三个内角之和为180°，即$\mathrm{\angle\:A\:+\:\angle\:B\:+\:\angle\:C\:=\:180°}$

直角三角形的作图

要作一个直角三角形，我们需要三角形的两条边的长度。这两条边中，一条必须是斜边，另一条必须是其他两条边中的一条。因为我们需要在一个角上画一个直角三角形，$\mathrm{\angle\:PQR\:is\:90°}$

已知两条边

当给出两条非斜边时，作直角三角形的步骤如下：

画一个直角三角形，底边长8厘米，高6厘米。

步骤1 - 画一条线段LM = 8厘米

步骤2 - 使用圆规，以L为圆心画弧，与线的两侧相交。

步骤3 - 画两条相交的弧。

步骤4 - 连接LZ，画一条90°的垂线。

步骤5 - 圆规量取6厘米，从L点画弧，标记为N。

步骤6 - 画一条连接N和M的线。

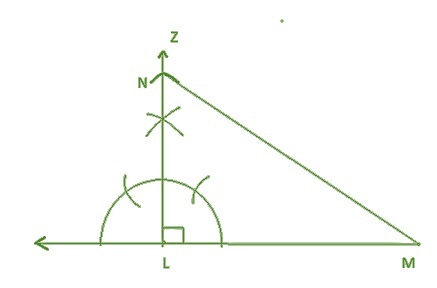
已知底边和斜边

已知底边和斜边作直角三角形的步骤如下：

已知PR = 7厘米，QR = 5厘米。作一个直角三角形∆PQR，直角为$\mathrm{\angle\:Q}$

步骤1 - 画一条线，取两点QR，使得QR = 5厘米

步骤2 - 使用圆规，以任意长度，从Q点为圆心在直线的两侧画两条弧。

步骤3 - 量取大于Q点一半的长度，画两条弧。

步骤4 - 连接弧的中心点和Q点，画一条QZ线，长度为90°。

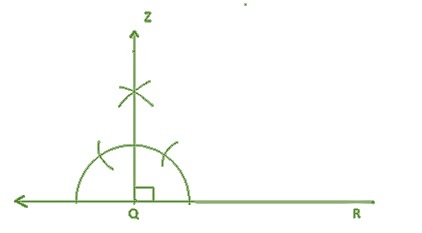
步骤5 - 将圆规设置为7厘米，以R为圆心在QZ线上画弧。

步骤6 - 标记中点P，现在画线PR。

已知底边和底角

作一个直角三角形LMN，底边为9厘米，底角为60°。

步骤1 - 画一条线段LM，使得LM = 9厘米

步骤2 - 画一条垂直线XLM= 90°

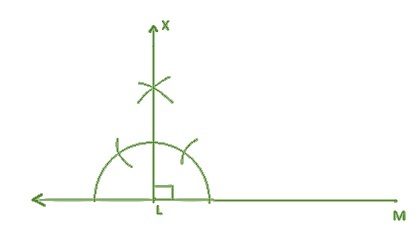
步骤3 - 使用圆规画弧，画一个60°角$\mathrm{\angle\:ZRQ\:=\:60°}$。

步骤4 - 从60°延伸一条线，连接线段LX形成MN。

由给定的底边和底角形成一个直角三角形LMN。

已知底边和非底角

只用直尺和圆规作一个直角三角形，已知底边AB = 5厘米，对边角 = 45°

$\mathrm{三个角的和\:=\:180°}$

$\mathrm{45°\:+\:90°\:+\:x\:=\:180°}$

$\mathrm{x\:=\:45°}$

底边的另一个角是45°

步骤1 - 画一条长度为AB = 5厘米的线段。

步骤2 - 从$\mathrm{\angle\:A\:=\:90°}$画一条垂直线

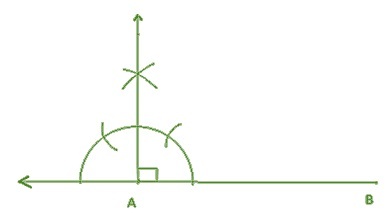
步骤3 - 将圆规放在B点，画另一条垂直线。

步骤4 - 要画一个$\mathrm{\angle\:B\:=\:45°}$角，用相同的长度，将圆规放在ZB线段上的弧上，画一条弧

步骤5 - 同样地，将圆规放在AB线段上的弧上画另一条弧。

步骤6 - 延伸这条线以画出连接AX线的BC线。

形成了一个直角三角形ABC。

例题

1. 求缺失边的值

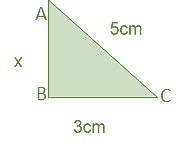
解

为了找到未知边，我们必须应用勾股定理，

$\mathrm{AC^{2}\:=\:AB^{2}\:+\:BC^{2}}$

$\mathrm{(5)^{2}\:=\:x^{2}\:+\:(3)^{2}}$

$\mathrm{25\:=\:x^{2}\:+\:9}$

$\mathrm{x\:=\:4cm}$

2. 如果只给出两个角$\mathrm{\angle\:A\:=\:50°\:and\:\angle\:C\:=\:40°}$，求三角形的类型

解

求三角形的另一边

三角形三个内角之和为180°

即，$\mathrm{\angle\:A\:+\:\angle\:B\:+\:\angle\:C\:=\:180°}$

$\mathrm{50\:+\:x\:+\:40\:=\:180}$

$\mathrm{x\:=\:90°}$

形成的三角形是直角三角形。

结论

直角三角形具有邻边、对边和斜边。它有3个角，其中一个必须是90°。使用直尺和圆规可以根据边和角的不同方式构造直角三角形。使用垂直平分线的作图方法，我们可以画出90°。

常见问题

1. 求直角三角形面积的公式是什么？

直角三角形的面积与三角形的面积相同

$\mathrm{直角三角形面积\:=\:\frac{1}{2}(底边\:\times\:高)}$

2. 如何在不使用量角器的情况下在三角形中画出45°？

将圆规放在一个点上并画一条弧，命名为弧。在所画的弧上，画两条弧。现在画两条相交的弧。画一条线连接这些点。

3. 如何识别直角三角形中的边？

直角三角形中最长的边，也就是斜线，是斜边。其他两个角根据所取的角而变化。与角相邻的边是邻边，另一边是对边。

4. 直角三角形中哪条边与90°相对？

斜边是三角形中最长的边，与直角相对。

5. 直角三角形中是否有钝角？

钝角大于90°。直角中有一个90°，其他两边的和必须等于90°。直角三角形有两个锐角和一个直角。