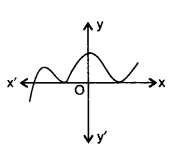
下图给出了某些多项式 $y = p(x)$ 的图像。在每种情况下，求 $p(x)$ 的零点个数。
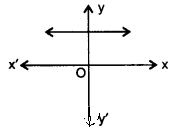
(i)
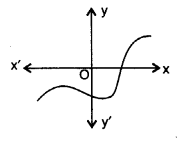
(ii)
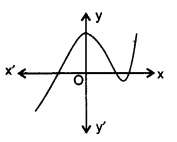
(iii)
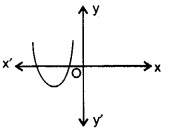
(iv)
(v)
(vi)
"
待办事项
我们必须在每种情况下找到 $p(x)$ 的零点个数。
解答
(i) 给定的图像在任何点都不与 x 轴相交。因此，零点个数为 $0$。
(ii) 图像在一点与 x 轴相交。因此，零点个数为 $1$。
(iii) 图像在三点与 x 轴相交。因此，零点个数为 $3$。
(iv) 图像在两点与 x 轴相交。因此，零点个数为 $2$。
(v) 图像在 $4$ 点与 x 轴相交。因此，零点个数为 $4$。
(vi) 图像在 $3$ 点与 x 轴相交。因此，零点个数为 $3$。
- 相关文章
- 下图 2.10 给出了某些多项式 \( p(x) \) 的图像 \( y=p(x) \)。在每种情况下，求 \( p(\bar{x}) \) 的零点个数。"
- 求下列每个多项式的 \( p(0), p(1) \) 和 \( p(2) \)：(i) \( p(y)=y^{2}-y+1 \)(ii) \( p(t)=2+t+2 t^{2}-t^{3} \)(iii) \( p(x)=x^{3} \)(iv) \( p(x)=(x-1)(x+1) \)
- 在下列每种情况下，求多项式的零点：(i) \( p(x)=x+5 \)(ii) \( p(x)=x-5 \)(iii) \( p(x)=2 x+5 \)(iv) \( p(x)=3 x-2 \)(v) \( p(x)=3 x \)(vi) \( p(x)=a x, a ≠ 0 \)(vii) \( p(x)=c x+d, c ≠ 0, c, d \) 是实数。
- 如果 \( x-1 \) 是下列每种情况下 \( p(x) \) 的一个因子，求 \( k \) 的值：(i) \( p(x)=x^{2}+x+k \)(ii) \( p(x)=2 x^{2}+k x+\sqrt{2} \)(iii) \( p(x)=k x^{2}-\sqrt{2} x+1 \)(iv) \( p(x)=k x^{2}-3 x+k \)
- 验证下列值是否为与其对应的多项式的零点。(i) \( p(x)=3 x+1, x=-\frac{1}{3} \)(ii) \( p(x)=5 x-\pi, x=\frac{4}{5} \)(iii) \( p(x)=x^{2}-1, x=1,-1 \)(iv) \( p(x)=(x+1)(x-2), x=-1,2 \)(v) \( p(x)=x^{2}, x=0 \)(vi) \( p(x)=l x+m, x=-\frac{m}{l} \)(vii) \( p(x)=3 x^{2}-1, x=-\frac{1}{\sqrt{3}}, \frac{2}{\sqrt{3}} \)(viii) \( p(x)=2 x+1, x=\frac{1}{2} \)
- 找出下列各项中的一项式、二项式和三项式：(i) \( 2 x+y-z \)(ii) \( -2 x^{3} \)(iii) \( -7-p \)(iv) \( 5 x y z \)(v) \( 5-3 y-y^{2} \)(vi) \( m^{2}-1 \)
- 对于 \( a \) 和 \( b \) 的哪些值，\( q(x)=x^{3}+2 x^{2}+a \) 的零点也是多项式 \( p(x)=x^{5}-x^{4}-4 x^{3}+3 x^{2}+3 x+b \) 的零点？\( p(x) \) 的哪些零点不是 \( q(x) \) 的零点？
- 从下列选项中，选择其图像分别为图 4.6 和图 4.7 的方程。对于图 4.6 (i) \( y=x \)(ii) \( x+y=0 \)(iii) \( y=2 x \)(iv) \( 2+3 y=7 x \) 对于图 4.7 (i) \( y=x+2 \)(ii) \( y=x-2 \)(iii) \( y=-x+2 \)(iv) \( x+2 y=6 \) "
- 用多项式 \( g(x) \) 除多项式 \( p(x) \)，在下列每种情况下求商和余数：(i) \( p(x) = x^3 - 3x^2 + 5x -3, g(x) = x^2-2\)(ii) \( p(x) =x^4 - 3x^2 + 4x + 5, g(x) = x^2 + 1 -x\)(iii) \( p(x) = x^4 - 5x + 6, g(x) = 2 -x^2\)
- 求多项式 \( x^{2}+x-p(p+1) \) 的零点。
- 在给定的图形中，检查 \( x+y=p+q \) 是否成立。"
- 两种化学物质 X 和 Y 结合形成含有 X 和 Y 的产物 P，X + Y → P。X 和 Y 不能通过简单的化学反应分解成更简单的物质。关于物质 X、Y 和 P，下列哪些说法是正确的？P 是一种化合物 X 和 Y 是化合物 X 和 Y 是元素 P 具有固定组成 (a) (i)、(ii) 和 (iii)、(b) (i)、(ii) 和 (iv)(c) (ii)、(iii) 和 (iv) (d) (i)、(iii) 和 (iv)
- 给出满足除法算法的多项式 \( p(x), g(x), q(x) \) 和 \( r(x) \) 的例子，并且 (i) deg \( p(x) = \) deg \( q(x) \) (ii) deg \( q(x) = \) deg \( r(x) \) (iii) deg \( r(x) = 0 \)
- 利用因式定理确定 \( g(x) \) 是否为下列每种情况下 \( p(x) \) 的因式：(i) \( p(x)=2 x^{3}+x^{2}-2 x-1, g(x)=x+1 \)(ii) \( p(x)=x^{3}+3 x^{2}+3 x+1, g(x)=x+2 \)(iii) \( p(x)=x^{3}-4 x^{2}+x+6, g(x)=x-3 \)
- 对于下列方程组，求 \( p \) 的值：\( -x+p y=1 \) 和 \( p x-y=1 \)，如果方程组无解。
数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学