数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
已知：点\( A\left(x_{1}, y_{1}\right), \mathrm{B}\left(x_{2}, y_{2}\right) \) 和 \( \mathrm{C}\left(x_{3}, y_{3}\right) \) 是\( \Delta \mathrm{ABC} \) 的顶点。求解：我们必须找到三角形 ABC 的重心的坐标。解：我们知道，三角形重心的坐标 = \(\left(\frac{\text { 所有顶点的横坐标之和}}{3}, \frac{\text { 所有顶点的纵坐标之和}}{3}\right)\)因此，三角形 ABC 的重心的坐标 = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)
已知：点 $A (1, -2), B (2, 3), C (a, 2)$ 和 $D (-4, -3)$ 构成一个平行四边形。求解：我们必须找到 $a$ 的值和平行四边形以 $AB$ 为底的高。解：从 \( \mathrm{D} \) 向 \( \mathrm{AB} \) 作垂线，垂足为 \( \mathrm{P} \)。\( \mathrm{DP} \) 是平行四边形的高。我们知道，平行四边形的对角线互相平分。这意味着，$AC$ 的中点 = $BD$ 的中点。连接点 \( \left(x_{1}, y_{1}\right) \) 和 \( \left(x_{2}, y_{2}\right) \) 的线段的中点是 \( (\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}) \)\( (\frac{1+a}{2}, ... 阅读更多
"
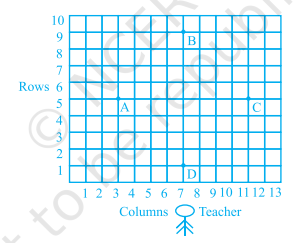
已知：学校的学生在操场上排成行排成列进行操练。\( \mathrm{A}, \mathrm{B}, \mathrm{C} \) 和 \( \mathrm{D} \) 是四个学生的位置。求解：我们必须找到是否可以在操练中安排贾斯帕尔的位置，使他与四个学生\( A, B, C \) 和 D 等距。解：从图中，我们观察到四个学生 A、B、C 和 D 的位置分别是 (3, 5)、(7, 9)、(11, 5) 和 (7, 1)。四个顶点构成一个四边形。\(AB ... 阅读更多
"
从给定的速度-时间图中，初始速度 $v_1=80\ ms^{-1}$，最终速度 $v_2=0$，时间 $t_1=0$，时间 $t_2=8\ s$。球的加速度 $a=\frac{速度变化(v_2-v_1)}{时间(t_2-t_1)}$$=\frac{0-80}{8-0}$$=\frac{-80}{8}$$=-10\ m/s^2$。如给定，球的质量 $m=50\ gm=0.05\ kg$ [因为 $1\ kg=1000\ g$]因此，地板对球提供的摩擦力 $F=ma$$=0.05\ kg\times -10\ m/s^2$$=-0.5\ N$ [$-ve$ 符号表示相反方向]因此，地板的摩擦力为 $0.05\ N$。
已知：电子的初始速度 $u=5\times 10^4\ ms^{-1}$，加速度 $a=10^4\ m s^{-2}$。求解：$(i)$。计算电子获得其初始速度两倍的速度所需的时间。$(ii)$。了解在此时间内电子所覆盖的距离。解：$(i)$。由于电子将获得其初始速度的两倍，因此其最终速度 $v=2u=2\times5\times 10^4\ ms^{-1}=10^5\ ms^{-1}$。使用第一运动方程，$v=u+at$$10^5\ ms^{-1}=5\times 10^4\ ms^{-1}+10^4\ m s^{-2}\times t$或 $10^5-5\times10^4=10^4\ m s^{-2}\times t$或 $5\times10^4=10^4t$或 $t=\frac{5\times10^4}{10^4}$或 $t=5\ 秒$因此，电子将在 5 秒内获得其初始速度的两倍。$(ii)$。使用第二运动方程，... 阅读更多
设 $u\ m/s$ 为以均匀加速度 $a$ 运动的物体的初速度。我们知道，第二运动方程，$s=ut+\frac{1}{2}at^2$这里，$u\rightarrow$ 初速度，$t\rightarrow$ 时间，$a\rightarrow$ 加速度，$s\rightarrow$ 行进距离。所以，第 4 秒内行进的距离 $s_{4th}=u\times4+\frac{1}{2}a\times4^2$$s_{4th}=4u+8a$类似地，$s_{5th}=u\times5+\frac{1}{2}a\times5^2$或 $s_{5th}=5u+\frac{25}{2}a$所以，第 4 秒和第 5 秒之间行进的距离 $=s_{5th}-s_{4th}$$=(5u+\frac{25}{2}a)-(4u+8a)$$=u+\frac{9}{2}a$
在这种情况下，加速度将向下为 'g'我们知道，$v^{2} \ =\ u^{2} \ - \ 2gh$ 或 $ h = \frac{u^{2} \ -\ v^{2}}{2g}$但在最高点，$v\ =\ 0$因此，$h\ =\ \frac{u^{2}}{2g}$对于第一个球，$h_{1} \ =\ \frac{u^{2}_{1}}{2g}$对于第二个球，$h_{2} \ =\ \frac{u^{2}_{2}}{2g}$如果我们除以 $h_{1}$ 和 $h_{2}$，那么我们将得到，$\frac{h_{1}}{h_{2}} \ =\ \frac{\frac{u^{2}_{1}}{2g}}{\frac{u^{2}_{2}}{2g}}=\frac{u^{2}_{1}}{u^{2}_{2}}$因此，$h_{1} :\ h_{2} \ =\ u^{2}_{1} \ :\ u^{2}_{2}$。
沿直线路径以加速运动的物体并不总是远离地球。因此，说法 $(c)$ 是不正确的。
守门员接住板球后会把手向后拉。这使守场员能够减少球施加的力。因此，选项 $(b)$ 是正确的。
火车上的一名乘客抛出一枚硬币，硬币落在他身后。这表明火车正在加速运动。因此，选项$(a)$是正确的。