数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律研究
包裹在铝管周围的纸不容易着火，因为铝金属是良好的导热体，因此热量会被传导走。此外，纸的燃点低于铝的燃点。当纸包裹在铝管周围时，燃点会升高。这就是为什么纸本身很容易着火，而包裹在铝管周围的纸却不容易着火。
蜡烛火焰的黄色部分是中间部分，阿比达将烧杯放在那里。由于该区域的空气不足以燃烧，因此燃料蒸气在此区域部分燃烧。燃料在中间区域的部分燃烧会产生碳颗粒。它的温度适中。因此，阿比达的烧杯需要一段时间才能加热。拉梅什的烧杯放在火焰的最外层。在这个区域，由于周围有充足的空气，因此燃料会完全燃烧。最外层区域是火焰中温度最高的区域... 阅读更多
(a) 碳酸氢钠（碳酸氢钠）(b) 火的热量会分解碳酸氢钠，产生二氧化碳气体。这种二氧化碳像毯子一样覆盖火焰，切断燃烧物质的新鲜空气供应。因此，火被熄灭。(c) 碳酸氢钾（或碳酸氢钾）
(a) 白磷在室温下在空气中燃烧属于自燃。自燃是指物质在没有明显原因的情况下突然燃烧的现象。(b) 液化石油气的燃烧属于借助外来热源，物质快速燃烧并产生热量和光亮的燃烧。(c) 引爆鞭炮属于借助热量或压力，物质突然燃烧并产生热量、光亮和声音的燃烧。(d) 煤矿中的煤尘燃烧属于自燃。
已知：$AD$ 是三角形 $ABC$ 的中线。$G$ 是中线 $AD$ 的中点。要证明：三角形 $ADB$ 和 $ADC$ 的面积相等，以及 $ar(\triangle BGC) = 2ar(\triangle AGC)$。证明：连接 $BG$ 和 $CF$。作 $AL \perp BC$$\mathrm{AD}$ 是 $\triangle \mathrm{ABC}$ 的中线这意味着，$\mathrm{BD}=\mathrm{DC}$$\operatorname{ar}(\triangle \mathrm{ABD})=\frac{1}{2}$ 底 $\times$ 高$=\frac{1}{2} \mathrm{BD} \times \mathrm{AL}$.........(i)$\operatorname{ar}(\triangle \mathrm{ACD})=\frac{1}{2} \times \mathrm{CD} \times \mathrm{AL}$$=\frac{1}{2} \times \mathrm{BD} \times \mathrm{AL}$.............(ii) (因为 $\mathrm{BD}=\mathrm{DC}$)从 (i) 和 (ii) 可以得出，$\operatorname{ar}(\triangle \mathrm{ABD})=\operatorname{ar}(\triangle \mathrm{ACD})$在 $\triangle \mathrm{BGC}$ 中，$\mathrm{GD}$ 是中线。$\operatorname{ar}(\triangle \mathrm{BGD})=\operatorname{ar}(\triangle \mathrm{CGD})$同样地，在 $\triangle \mathrm{ACD}$ 中，$\mathrm{G}$ 是 $\mathrm{AD}$ 的中点，$\mathrm{CG}$ 是中线。$\operatorname{ar}(Delta \mathrm{AGC})=\operatorname{ar}(\Delta \mathrm{CGD})$从 (i) ... 阅读更多
"\已知：$ABCD, ABFE$ 和 $CDEF$ 是平行四边形。要证明：$ar(\triangle ADE) = ar(\triangle BCF)$。证明：$ABCD$ 是平行四边形。这意味着，$AD = BC$同样地，在平行四边形 $ABEF$ 中，$AE = BF$在平行四边形 $CDEF$ 中，$DE = CF$在 $\triangle ADE$ 和 $\triangle BCF$ 中，$AD = BC$$DE = CF$$AE = BF$因此，根据 SSS 公理，$\triangle ADE \cong \triangle BCF$这意味着，$ar(\triangle ADE) = ar(\triangle BCF)$ (全等三角形的面积相等)证毕。
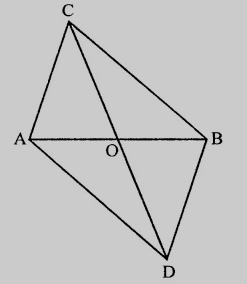
"\已知：$ABC$ 和 $ABD$ 是以 $AB$ 为底的两个三角形。线段 $CD$ 被 $AB$ 在 $O$ 点平分。要证明：$ar(\triangle ABC) = ar(\triangle ABC)$。证明：$CO = OD$作 $CL \perp AB$ 和 $DM \perp AB$在 $\Delta CLO$ 和 $\triangle D M O$ 中，$\angle \mathrm{L}=\angle \mathrm{M}$$\mathrm{CO}=\mathrm{OD}$$\angle \mathrm{COL}=\angle \mathrm{DOM}$ (对顶角)因此，根据 AAS 公理， $\Delta CLO \cong \triangle D M O$这意味着，$\mathrm{CL}=\mathrm{DM}$ (全等三角形对应边相等)$ar(\triangle \mathrm{ABC})=\frac{1}{2}\times$ 底 $\times$ 高$=\frac{1}{2} \times \mathrm{AB} \times \mathrm{CL}$.........(i)$ar(\triangle \mathrm{ADB})=\frac{1}{2} \times \mathrm{AB} \times \mathrm{DM}$$=\frac{1}{2} \mathrm{AB} \times \mathrm{CL}$...........(ii) ... 阅读更多
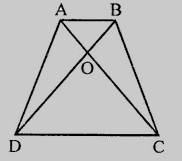
"\已知：$ABCD$ 是一个梯形，其中 $AB \parallel DC$。要证明：$ar( \triangle AOD = ar(\triangle BOC)$。证明：在梯形 $ABCD$ 中，对角线 $AC$ 和 $BD$ 相交于 $O$ 点。$\triangle ADB$ 和 $\triangle ACB$ 同底 $AB$ 且在同一对平行线之间。因此，$ar(\triangle ADB = ar(\triangle ACD)$从等式两边减去 $ar(\triangle AOB)$，$ar(\triangle ADB) - ar(\triangle AOB) = ar(\triangle ACD) - ar(\triangle AOB)$$ar(\triangle AOD) = ar(\triangle BOC)$证毕。
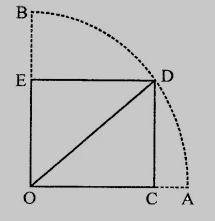
"\已知：$OCDE$ 是一个内接于半径为 $10\ cm$ 的圆的四分之一圆的矩形。 $OE = 2\sqrt5$。要证明：求矩形的面积。证明：圆的四分之一圆的半径 $= 2\sqrt5$ 个单位矩形的对角线 = 10 个单位 ($OD = OB = OA = 10\ cm$)$DE = 2\sqrt5\ cm$在 $\triangle OED$ 中，$OD^2 = OE^2 + DE^2$$10^2 = OE^2 + (2\sqrt5)^2$$100 = OE^2 + 20$$OE^2 = 100 - 20$$ = 80$$OE^2 = (4\sqrt5)^2$$\Rightarrow OE = 4\sqrt5\ cm$矩形的面积 $= l \times b$$= DE \times OE$$= 2\sqrt5 \times 4\sqrt5$$= 8 \times 5$$= 40\ cm^2$矩形的面积为 $40\ cm^2$。
"\已知：$\angle AOB = 90^o, AC = BC, OA = 12\ cm$ 和 $OC = 6.5\ cm$。要证明：求 $\triangle AOB$ 的面积。证明：$C$ 是斜边的中点。这意味着，$AC = CB = OC = 6.5\ cm$$AB = 6.5 + 6.5$$= 13\ cm$在 $\triangle AOB$ 中，$AB^2 = AO^2 + OB^2$ (勾股定理)$(13)^2 = (12)^2 + OB^2$$169 = 144 + OB^2$$OB^2 = 169 - 144$$= 25$$= 5^2$$\Rightarrow OB = 5\ cm$ $\Delta \mathrm{AOB}$ 的面积$=\frac{1}{2}\times$ 底 $\times$ 高$=\frac{1}{2} \times \mathrm{OB} \times \mathrm{AO}$$=\frac{1}{2} \times 5 \times 12$$=30 \mathrm{~cm}^{2}$