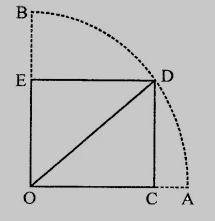
如图所示，矩形$OCDE$内接于半径为$10\ cm$的圆的四分之一圆弧中。如果$OE = 2\sqrt5$，求矩形的面积。
"\n

已知

矩形$OCDE$内接于半径为$10\ cm$的圆的四分之一圆弧中。

$OE = 2\sqrt5$。

要求

我们需要求出矩形的面积。

解答

圆的四分之一圆弧的半径$= 2\sqrt5$ 个单位

矩形的对角线 = 10 个单位          ($OD = OB = OA = 10\ cm$)

$DE = 2\sqrt5\ cm$

在$\triangle OED$中，

$OD^2 = OE^2 + DE^2$

$10^2 = OE^2 + (2\sqrt5)^2$

$100 = OE^2 + 20$

$OE^2 = 100 - 20$

$ = 80$

$OE^2 = (4\sqrt5)^2$

$\Rightarrow OE = 4\sqrt5\ cm$

矩形的面积 $= l \times b$

$= DE \times OE$

$= 2\sqrt5 \times 4\sqrt5$

$= 8 \times 5$

$= 40\ cm^2$

矩形的面积为$40\ cm^2$。

教程点

更新于: 2022年10月10日

51 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习