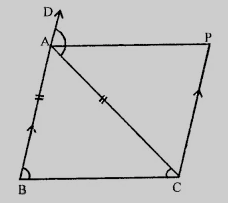
已知:如图所示,$AB = AC$,$CP \parallel BA$,$AP$ 是$\triangle ABC$外角$\angle CAD$的平分线。求证:$ABCP$是平行四边形。证明:在$\triangle ABC$中,$AB = AC$,则$\angle C = \angle B$ (等边对等角) $\angle CAD = \angle B + \angle C = \angle C + \angle C = 2\angle C$……(i) $AP$是$\angle CAD$的平分线,则$2\angle PAC = \angle CAD$……(ii) 由(i)和(ii)得,$\angle C = 2\angle PAC$,$\angle C = \angle CAD$,$\angle BCA = \angle PAC$,$\angle PAC$和… 阅读更多
已知:如图所示,$AB = AC$,$CP \parallel BA$,$AP$ 是$\triangle ABC$外角$\angle CAD$的平分线。求证:$\angle PAC = \angle BCA$。证明:在$\triangle ABC$中,$AB = AC$,则$\angle C = \angle B$ (等边对等角) $\angle CAD = \angle B + \angle C = \angle C + \angle C = 2\angle C$……(i) $AP$是$\angle CAD$的平分线,则$2\angle PAC = \angle CAD$……(ii) 由(i)和(ii)得,$\angle C = 2\angle PAC$,$\angle C = \angle CAD$,$\angle BCA = \angle PAC$。因此,… 阅读更多
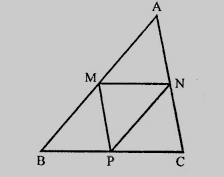
已知:如图所示,$M、N、P$分别是$AB、AC、BC$的中点。$MN = 3cm,NP = 3.5cm,MP = 2.5cm$。求解:$BC、AB、AC$的长度。解:$MN=3cm,NP=3.5cm,MP=2.5cm$。$M$和$N$分别是$AB$和$AC$的中点,则$MN \parallel BC$且$MN=\frac{1}{2}BC$,$\Rightarrow 3=\frac{1}{2}BC$,$BC=6cm$。同理,$NP=\frac{1}{2}AB$,$\Rightarrow AB=2 \times NP = 2 \times 3.5 = 7cm$,$MP=\frac{1}{2}AC$,$\Rightarrow AC=2 \times MP = 2 \times 2.5 = 5cm$。因此,$BC=6cm,AB=7cm,AC=5cm$。阅读更多
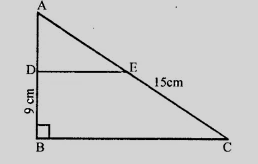
已知:如图所示,三角形$ABC$在$B$处成直角,$AB = 9cm,AC = 15cm$,$D、E$分别是边$AB$和$AC$的中点。求解:$BC$的长度。解:在$\triangle ABC$中,$\angle B=90^\circ$,$AC^2 = AB^2 + BC^2$ (勾股定理),$\Rightarrow BC^2 = AC^2 - AB^2 = (15)^2 - (9)^2 = 225 - 81 = 144 = (12)^2$,$BC = 12cm$。
已知:在$\triangle ABC$中,$BM$和$CN$分别是$B$和$C$到过$A$的任意直线的垂线。$L$是$BC$的中点。求证:$ML=NL$。证明:连接$ML$和$NL$。在$\triangle BMP$和$\triangle CNP$中,$\angle M = \angle N = 90^\circ$,$\angle BPM = \angle CPN$ (对顶角)。因此,根据AA相似性公理,$\triangle BML \sim \triangle LMC$。则$\frac{BM}{CN} = \frac{PM}{PN}$。在$\triangle BML$和$\triangle CNL$中,$\frac{BM}{CN} = \frac{PM}{PN}$,$\angle B = \angle C$ (内错角)。因此,$\triangle BML \sim \triangle LNC$。则$\frac{ML}{LN} = \frac{BL}{LC}$,$BL = LC$,则$CL$是$BL$的中点,$\frac{BL}{LC} = 1$,$\Rightarrow \frac{ML}{LN} = 1$,因此$ML = LN$。证毕。阅读更多
已知:在$\triangle ABC$中,$E$和$F$分别是$AC$和$AB$的中点。对$BC$作高$AP$,交$FE$于$Q$。求证:$AQ = QP$。证明:连接$EF$。作$AP \perp BC$,交$FE$于$Q$,交$BC$于$P$。在$\triangle ABC$中,$EF \parallel BC$且$EF = \frac{1}{2}BC$,$\angle F = \angle B$。在$\triangle ABP$中,$F$是$AB$的中点,$Q$是$FE$的中点,则$FQ \parallel BC$,$Q$是$AP$的中点,$AQ = QP$。证毕。阅读更多
已知:在$\triangle ABC$中,中线$AD$延长到$X$,使得$AD = DX$。求证:$ABXC$是平行四边形。证明:连接$BX$和$CX$。在$\triangle ABD$和$\triangle CDX$中,$AD = DX$,$BD = DC$,$\angle ADB = \angle CDX$ (对顶角)。因此,根据SAS公理,$\triangle ABD \cong \triangle CDX$。则$AB = CX$ (全等三角形的对应边相等),$\triangle ABD = \triangle DCX$,$\triangle ABD$和$\triangle DCX$是内错角,$AB \parallel CX$且$AB = CX$。因此,$ABXC$是平行四边形。
已知:在一个三角形中,$P、Q、R$分别是边$BC、CA、AB$的中点。$AC = 21cm,BC = 29cm,AB = 30cm$。求解:四边形$ARPQ$的周长。解:$P、Q、R$分别是边$BC、CA、AB$的中点,则$PQ \parallel AB$且$PQ = \frac{1}{2}AB = \frac{1}{2} \times 30 = 15cm$。同理,$QR \parallel BC$且$QR = \frac{1}{2}BC = \frac{1}{2} \times 29 = 14.5cm$,$RP \parallel AC$且$RP = \frac{1}{2}AC = \frac{1}{2} \times 21 = 10.5cm$。四边形$ARPQ$的周长$= AR + RP + PQ + AQ = \frac{1}{2}AB + \frac{1}{2}AC + \frac{1}{2}AB + \frac{1}{2}AC = AB + AC = 30 + 21 = 51cm$。… 阅读更多
燃料不完全燃烧会产生一种叫做一氧化碳的剧毒气体。
由于CNG(压缩天然气)产生的有害物质非常少,因此它正在逐步取代汽油和柴油作为汽车燃料。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP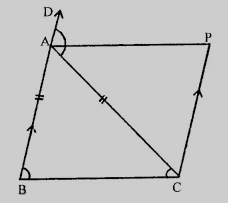 "\
"\
 "\
"\ "\
"\ "\
"\