如图所示，$AB = AC$，$CP \parallel BA$，$AP$ 是 $\triangle ABC$ 外角 $\angle CAD$ 的平分线。证明 $ABCP$ 是平行四边形。

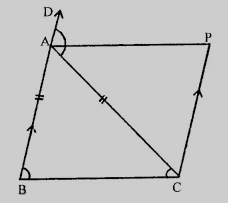
已知

如图所示，$AB = AC$，$CP \parallel BA$，$AP$ 是 $\triangle ABC$ 外角 $\angle CAD$ 的平分线。

要求

我们必须证明 $ABCP$ 是平行四边形。

解答

在 $\triangle ABC$ 中，

$AB = AC$

这意味着，

$\angle C = \angle B$ (等边对等角)

$\angle CAD = \angle B + \angle C$

$= \angle C + \angle C$

$= 2\angle C$.......….(i)

$AP$ 是 $\angle CAD$ 的平分线

这意味着，

$2\angle PAC = \angle CAD$.........…(ii)

由 (i) 和 (ii) 可得，

$\angle C = 2\angle PAC$

$\angle BAC = \angle CAD$ (此处应为$\angle BCA = \angle PAC$)

$\angle BCA = \angle PAC$

$\angle PAC$ 和 $\angle BCA$ 是内错角，

这意味着，

$AD \parallel BC$

$BA \parallel CP$

因此，

$ABCP$ 是平行四边形。

Tutorialspoint

更新于：2022年10月10日

48 次浏览

开启你的职业生涯

完成课程获得认证

开始学习