数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：\( P A \)和\( P B \)是从外部点\( P \)引出的切线。使得\( P A=10 \mathrm{~cm} \)和\( \angle A P B=60^{\circ} \)。要求：我们需要找到弦\( A B \)的长度。 解：从圆外一点引出的切线相等这意味着，$PA = PB = 10\ cm, \angle PAB = \angle PBA$ (等边对等角)在 $\triangle APB$ 中， $\angle APB + \angle PAB + \angle PBA = 180^o$$60^o + \angle PAB + \angle PAB = 180^o$$2 \angle PAB = 180^o - 60^o$$\angle PAB= ... 阅读更多
"\已知：\( P Q \)在圆心为\( O \)的圆的点\( R \)处相切。\( \angle T R Q=30^{\circ} \)。要求：我们需要找到\( m \angle P R S \)。解：在图中，连接 $RT$ 和 $RS$，使得 $\angle TRQ = 30^o$设 $\angle PRS = x^o$$\angle SRX = 90^o$（半圆上的角是 $90^o$)$\angle TRQ + \angle SRT + \angle PRS = 180^o$（一条直线上的角之和是 $180^o$)$30^o + 90^o + x^o = 180^o$$120^o + x^o = 180^o$$x^o = 180^o - 120^o$$x^o= 60^o$$\angle PRS = 60^o$因此，\( ... 阅读更多
已知：物体的质量，$m$ = 10 kg。高度，$h$ = 4.9 m。重力加速度，$g$ = 9.8 $m/s^2$。求：物体的速度，$v$。解：我们知道势能的公式为：- $P.E=mgh$代入给定值，我们得到：- $P.E=10\times {9.8}\times {4.9}$ $P.E=480.2J \sim 480J$$P.E=480J$现在，根据能量守恒定律，我们知道：-系统的总能量保持不变。$\therefore$物体刚接触地面时的动能等于 4.9 m 高度处的势能。$\therefore$动能 = 480 J。我们知道动能的公式为 ... 阅读更多
已知：$111-( 111-11)$。要求：解：$111-( 111-11)$。解： $111-( 111-11)$$=111-( 100)$$=11$因此，$111-( 111-11)=11$.
已知：$\frac{121\times121}{11\times11}$。要求：解：$\frac{121\times121}{11\times11}$。解：$\frac{121\times121}{11\times11}$$=11\times11$$=121$因此，$\frac{121\times121}{11\times11}=121$.
已知：$7,\ 3,\ -1,\ -5$, ____, ______, ______。要求：填空。解： 给定的模式：$7,\ 3,\ -1,\ -5$, ____, ______, ______。这是一个等差数列，这里 $d=3-7=-5-( -1)=-4$$\therefore 7,\ 3,\ -1,\ -5,\ \underline{-9},\ \underline{-13},\ \underline{-17}$。
已知：分数：$\frac{1}{2},\ \frac{4}{5},\ \frac{-2}{3},\ \frac{-1}{2},\ \frac{-5}{7}$。要求：将给定的分数按升序排列。解： 给定的分数：$\frac{1}{2},\ \frac{4}{5},\ \frac{-2}{3},\ \frac{-1}{2},\ \frac{-5}{7}$。分母 $2,\ 5,\ 3,\ 2,\ 7$ 的最小公倍数 $=210$$\frac{1}{2}=\frac{1}{2}\times\frac{55}{55}=\frac{55}{210}$$\frac{4}{5}=\frac{4}{5}\times\frac{42}{42}=\frac{168}{210}$$\frac{-2}{3}=\frac{-2}{3}\times\frac{70}{70}=\frac{-140}{210}$$\frac{-1}{2}=\frac{-1}{2}\times\frac{105}{105}=\frac{-105}{210}$$\frac{-5}{7}=\frac{-5}{7}\times\frac{30}{30}=\frac{-150}{210}$将给定的分数按升序排列：$\frac{-150}{210}
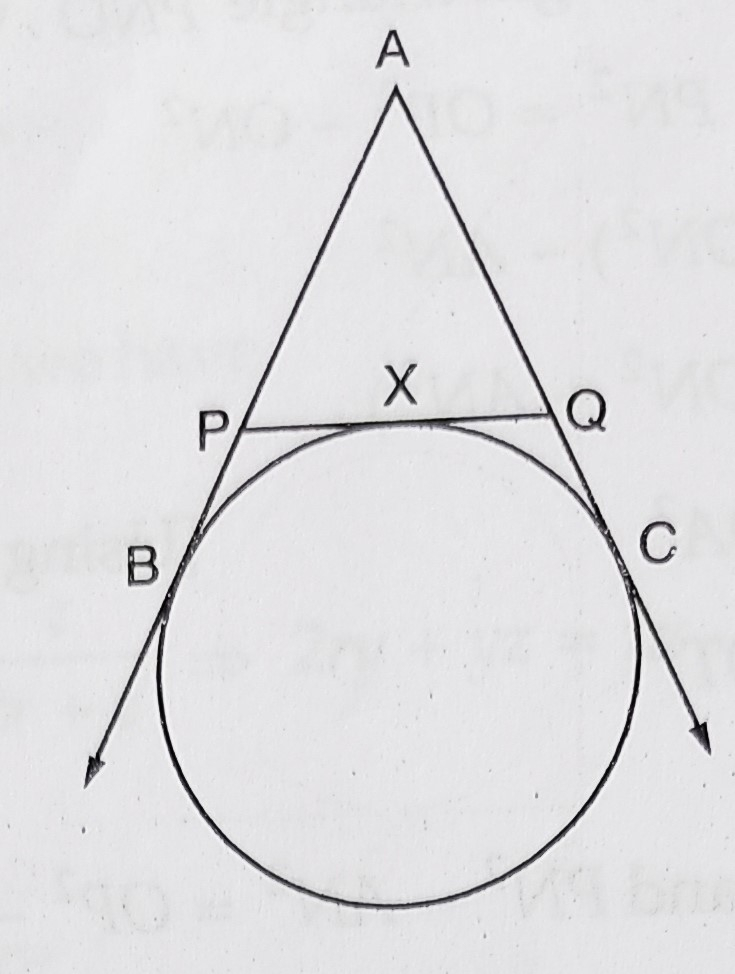
"\已知：AB、AC、PQ 是图中的切线，且 $AB = 5\ cm$。要求：我们需要找到 $\triangle APQ$ 的周长。解：从一个外点到圆的两条切线的长度相等。这意味着，PB 和 PX 是从 P 引出的切线。$PB = PX$类似地，QC 和 QX 是从 Q 引出的切线。$QC = QX$AB 和 AC 是从 A 引出的切线。$AB = AC$因此，$\triangle APQ$ 的周长 $= AP + PQ + AQ$$= AP + PX + QX + AQ$$= AP + PB + QC + AQ$ (因为 $PB = PX$ 和 $QC = ... 阅读更多
要求：我们需要证明圆的两条平行切线之间的切线段在圆心处构成一个直角。解：设 $PQ$ 和 $RS$ 是圆的两条平行切线。$RMP$ 是切线 $PQ$ 和 $RS$ 之间的切线段。连接 $RO$ 和 $PQ$，其中 $O$ 是圆心。$RL$ 和 $RM$ 是切线，连接 $\mathrm{RO}$。这意味着，$\angle LRO=\angle MRO$.......(i)类似地，$PM$ 和 $PN$ 是切线，连接 $\mathrm{PO}$。$\angle NPO=\angle MPO$.......(ii)将方程式 (i) 和 (ii) 相加，我们得到，$\angle LRO+\angle NPO=\angle MRO+\angle MPO$$\angle \mathrm{LRM}+\angle \mathrm{MPN}=180^{\circ}$ (内错角)$\Rightarrow \angle LRO+\angle MRO+\angle MPO+\angle ... 阅读更多
已知：$2+2-2\times2-9-( \frac{3}{2})$%=?要求：解：$2+2-2\times2-9-( \frac{3}{2})$%=?解： $2+2-2\times2-9-( \frac{3}{2})$%=?$=4-4-9-\frac{3}{2}\times100$$=-9-150$$=-159$因此，$2+2-2\times2-9-( \frac{3}{2})=-159$.