数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学
题目：我们需要证明在圆的切点处与切线垂直的直线经过圆心。解答：设 $TS$ 为以 $O$ 为圆心在 $P$ 点与圆相切的切线。连接 $OP$。画一条直线 $OR$，与圆相交于 $Q$ 点，并与切线 $TS$ 相交于 $R$ 点。$OP = OQ$ (圆的半径)$OQ \Rightarrow OP$ 同理，$OP$ 小于所有从 $O$ 点到 $TS$ 的直线。$OP$ 是最短的直线。因此，$OP$ 垂直于 $TS$。经过 $P$ 点的垂直线将经过圆心。因此……阅读更多
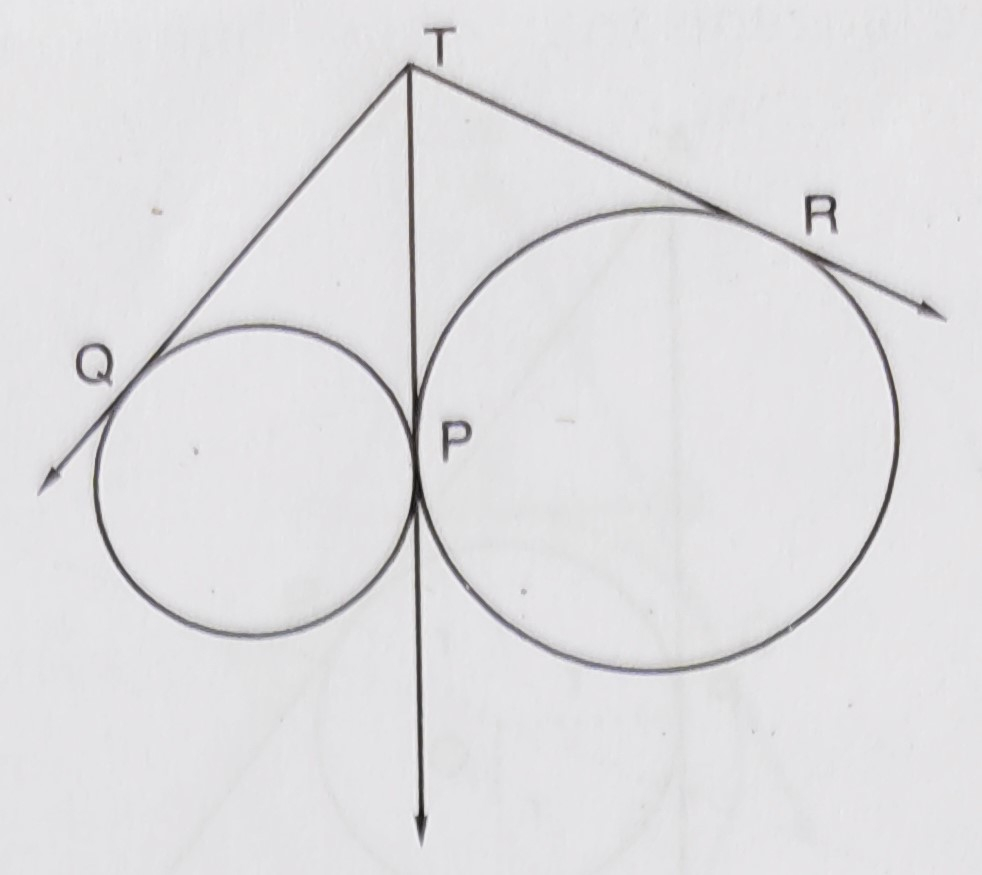
"\已知：两个圆在点 \( P \) 外切。从切线 \( P \) 上的一点 \( T \) 引出两个圆的切线 \( TO \) 和 \( TR \)，切点分别为 \( Q \) 和 \( R \)。题目：我们需要证明 \( TQ = TR \)。解答：从点 $T$，$TR$ 和 $TP$ 是到以 $O$ 为圆心的圆的两个切线。这意味着，$TR = TP$....….(i) 同理，从点 $T$，$TQ$ 和 $TP$ 是到以 $C$ 为圆心的圆的两个切线。$TQ = TP$...….(ii) 从 (i) 和 (ii)，我们得到，$TQ = TR$ 证毕。
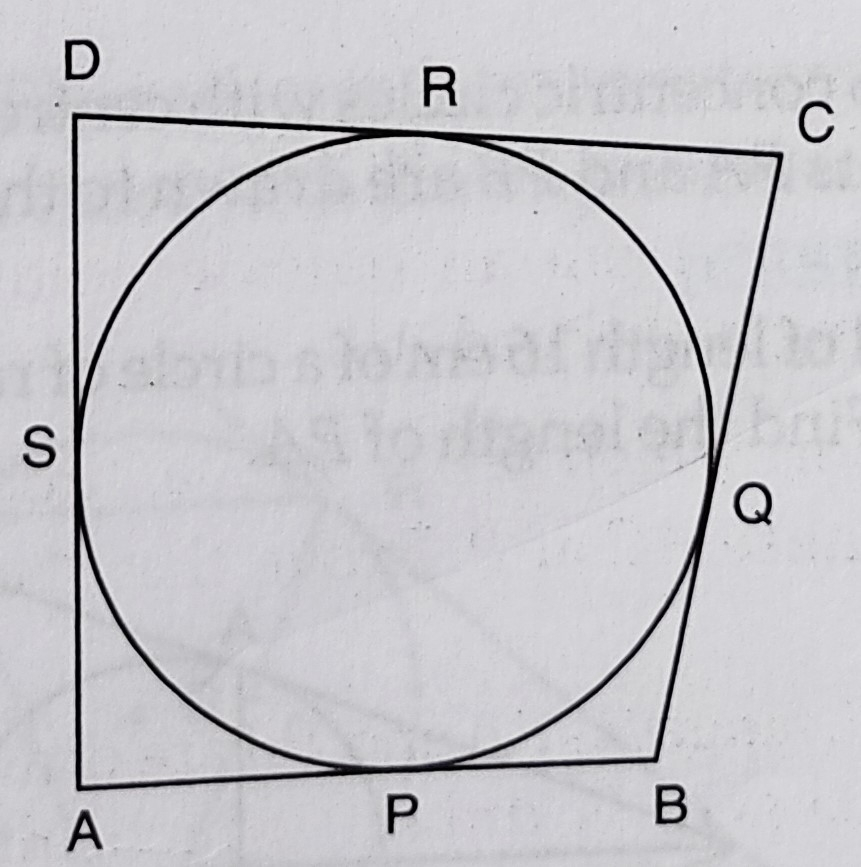
"\已知：一个圆与四边形 \( ABCD \) 的四条边相切，其中 \( AB=6 \mathrm{~cm} \)，\( BC=7 \mathrm{~cm} \)，\( CD=4 \mathrm{~cm} \)。题目：我们需要求 \( AD \)。解答：设 $AD = x$，$AP$ 和 $AS$ 是圆的切线。这意味着，$AP = AS$ 同理，$BP = BQ$，$CQ = CR$，$DR = DS$。因此，$AP+BP+DR+CR=AS+BQ+DS+CQ$，$AB + CD = AD + BC$，$6 + 4 = 7 + x$，$10 = 7 + x$，$x = 10 - 7$，$x= 3$。因此，$AD=3\ cm$。
已知：\( AB \) 是直径，\( AC \) 是以 \( O \) 为圆心的圆的弦，使得 \( \angle BAC=30^{\circ} \)。在 \( C \) 点的切线与 \( AB \) 相交于点 \( D \)。题目：我们需要证明 \( BC=BD \)。解答：连接 $BC$ 和 $OC$。$\angle BAC = 30^o$ $\Rightarrow \angle BCD = 30^o$ (切线与弦之间的角度等于弦在另一侧所成的角)$\angle ACD = \angle ACO + \angle OCD$ $\angle ACD ... 阅读更多
已知：\( \triangle ABC \) 是等腰三角形，\( AB=AC \)，\( C(O, r) \) 是 \( \triangle ABC \) 的内切圆，与 \( BC \) 相切于 \( L \)。题目：我们需要证明 \( L \) 平分 \( BC \)。解答：$AM$ 和 $AN$ 是从 $A$ 点引出的圆的切线。$AM = AN$，$AB = AC$ (已知)，$AB - AN = AC - AM$，$BN = CM$，$BL$ 和 $BN$ 是从 $B$ 点引出的切线，$BL = BN$ 同理，$CL$ 和 $CM$ 是从 $C$ 点引出的切线，$CL = CM$。因此，$CL=BL$ (因为 $BN = CM$ 且 $BN=BL$)。因此，$L$ 平分 $BC$。
已知：从点 \( P \) 引出两条切线 \( PA \) 和 \( PB \) 到以 \( O \) 为圆心的圆。\( OP= \) 圆的直径。题目：我们需要证明 \( \triangle APB \) 是等边三角形。解答：连接 $AB, OP, AQ, OA$。设 $r$ 为圆的半径。这意味着，$OP = 2r$，$OQ + QP = 2r$，$OQ = QP = r$。在直角三角形 $OAP$ 中，$OP$ 是斜边，$Q$ 是它的中点。$OA = AQ = OQ$ (直角三角形的斜边中点到三个顶点的距离相等)... 阅读更多
已知：两条切线段 \( PA \) 和 \( PB \) 引出到以 \( O \) 为圆心的圆，使得 \( \angle APB=120^{\circ} \)。题目：我们需要证明 \( OP=2AP \)。解答：连接 $OP$。取 $OP$ 的中点为 $M$，连接 $AM$。连接 $OA$ 和 $OB$。在直角三角形 $OAP$ 中，$\angle OPA = \frac{1}{2} \angle APB = \frac{1}{2}(120^o) = 60^o$，$\angle AOP = 90^o - 60^o = 30^o$，$M$ 是 $\triangle OAP$ 斜边 $OP$ 的中点。这意味着，$MO = MA = MP$，$\angle OAM = \angle AOM = 30^o$ $\angle ... 阅读更多
如图所示，\( ABC \) 是一个直角三角形，在 \( B \) 处成直角，\( BC=6 \mathrm{~cm} \) 和 \( AB=8 \mathrm{~cm} \)。求其内切圆的半径。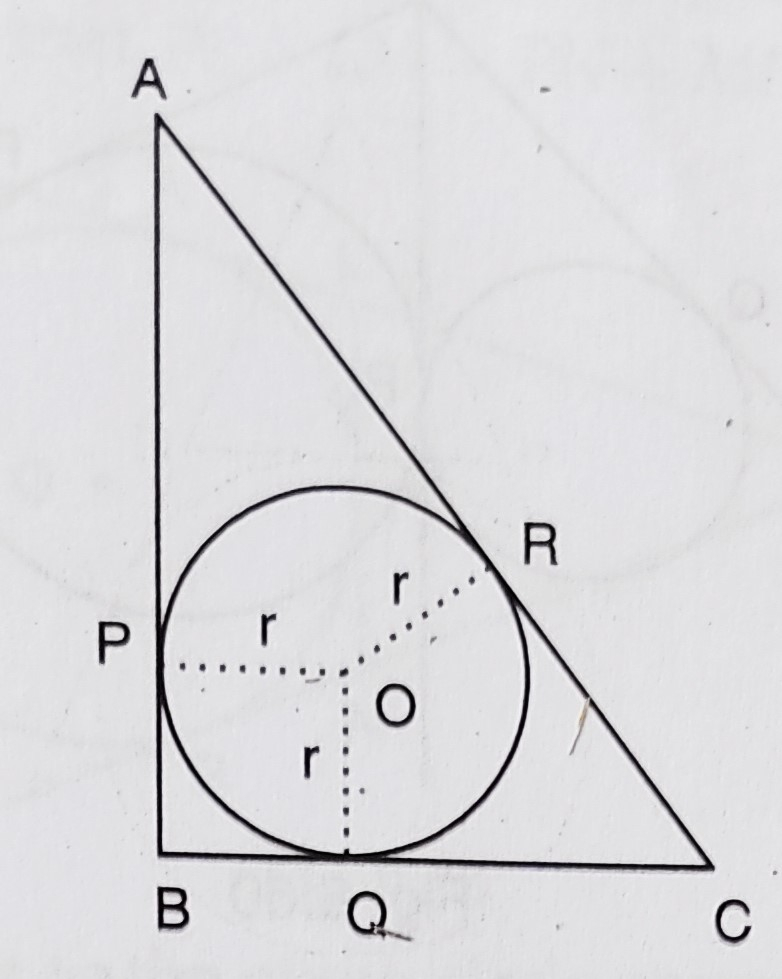
"\
已知：如图所示，\( ABC \) 是一个直角三角形，在 \( B \) 处成直角，\( BC=6 \mathrm{~cm} \) 和 \( AB=8 \mathrm{~cm} \)。题目：我们需要求其内切圆的半径。解答：在直角三角形 $ABC$ 中，$\angle B = 90^o, BC = 6\ cm, AB = 8\ cm$。设 $r$ 为内切圆的半径，其圆心为 $O$，并分别与边 $AB, BC$ 和 $CA$ 相切于 $P, Q$ 和 $R$。$AP$ 和 $AR$ 是圆的切线。这意味着，$AP = AR$ 同理，$CR = CQ$ 和 $BQ = BP$。$OP$ 和 $OQ$ 是…阅读更多
已知：在直角三角形ABC中，∠B=90°，以AB为直径作圆，交斜边AC于点P。 求证：在P点处作圆的切线平分BC。 解：设O为已知圆的圆心。设在P点的切线与BC交于点Q。连接BP。∠ABC = 90° (圆上任意一点的切线垂直于过该点的半径) 在△ABC中，∠CAB + ∠BCA = 90° ... 阅读更多
已知：从圆外一点P引圆的两条切线PA和PB，在圆上一点E处作切线，该切线分别与PA和PB交于C和D。PA=14cm。求证：求三角形PCD的周长。解：PA和PB是从圆外一点P引出的圆的两条切线，O为圆心。CD是圆在E点处的切线… 阅读更多