已知:图中显示了一个方形飞镖靶。较大正方形的边长是较小正方形边长的 1.5 倍。飞镖被投掷并落在较大正方形上。求解:我们需要找到它落在较小正方形内部的概率。解:设较小正方形的边长为 $a$ 个单位。这意味着,正方形 ABCD 的边长为 $1.5 \times a$ 个单位 $= \frac{3}{2}a$ 个单位。正方形 ABCD 的面积 $=(\frac{3 a}{2})^{2} = \frac{9}{4} a^{2}$ 平方单位。正方形 PQRS 的面积 $=a^{2}$ 平方单位。落在……阅读更多
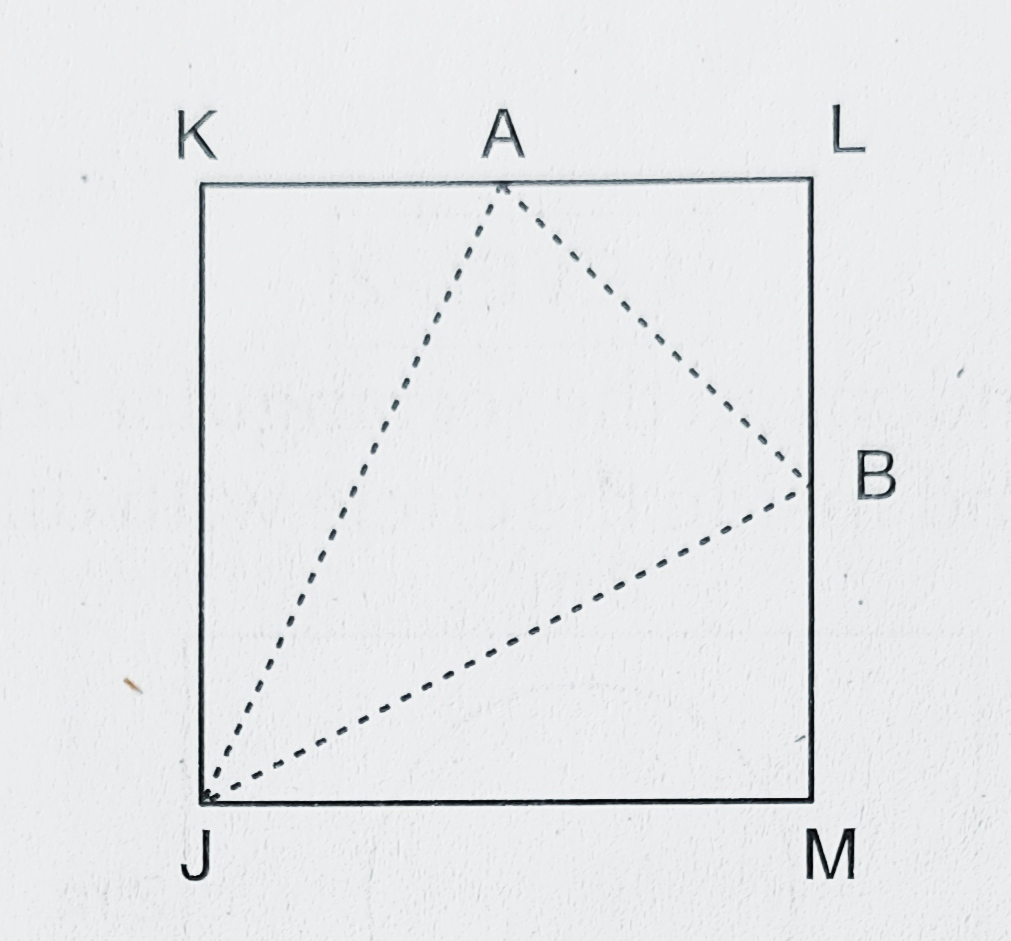
已知:图中,JKLM 是一个边长为 6 个单位的正方形。点 A 和 B 分别是边 KL 和 LM 的中点。从正方形内部随机选择一个点。求解:我们需要找到该点被选自三角形 JAB 内部的概率。解:正方形 JKLM 的边长 = 6 个单位,正方形的面积 = $(6)^{2} = 36$ 平方单位。A 和 B 分别是 KL 和 LM 的中点。$AL = AK = BM = BL = \frac{6}{2} = 3$ 个单位。三角形 AJK 的面积 $= \frac{JK \times AK}{2} = \frac{6 \times 3}{2} = 9$ 平方单位。三角形 JMB 的面积 $= \frac{JM \times MB}{2} = \frac{6 \times 3}{2} = 9$ 平方单位。三角形……阅读更多
氮原子 (147N) 中价电子的数量是 5(电子构型:2,5)。
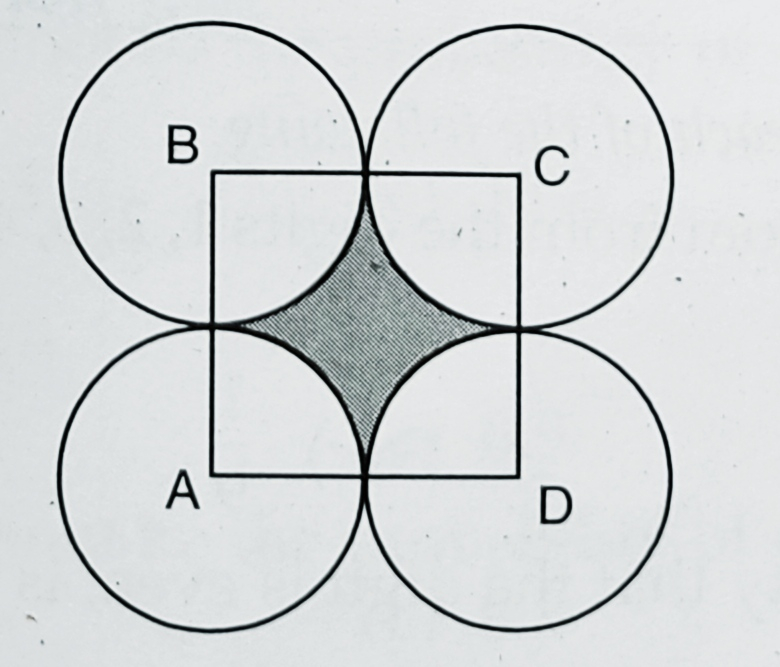
已知:在图中,点 A、B、C 和 D 是四个圆的圆心,每个圆的半径为一个单位长度。从正方形 ABCD 的内部随机选择一个点。求解:我们需要找到该点被选自阴影区域的概率。解:每个圆的半径 = 1 个单位,这意味着,正方形 ABCD 的边长 = 1+1=2 个单位。正方形的面积 = $2^{2} = 4$ 平方单位。正方形内部 A、B、C 和 D 处的四个象限的面积 = $4 \times \frac{1}{4} \pi r^{2} = \pi(1)^{2} = \pi$ 平方单位,这意味着,阴影区域的面积 = $4-\pi$ 平方单位。因此,飞镖落在阴影区域的概率 = 阅读更多
感应电流是指在导体周围变化的磁场中产生的导体中的电流。解释:线圈中磁力线的变化是线圈中感应电流的原因,这种现象称为电磁感应。电磁感应是一个过程,其中放置在变化的磁场中的导体(或穿过静止磁场的导体)会在电导体上产生电动势(电压)。电磁感应的过程也可以反向工作,因此运动的电荷会产生磁场。阅读更多
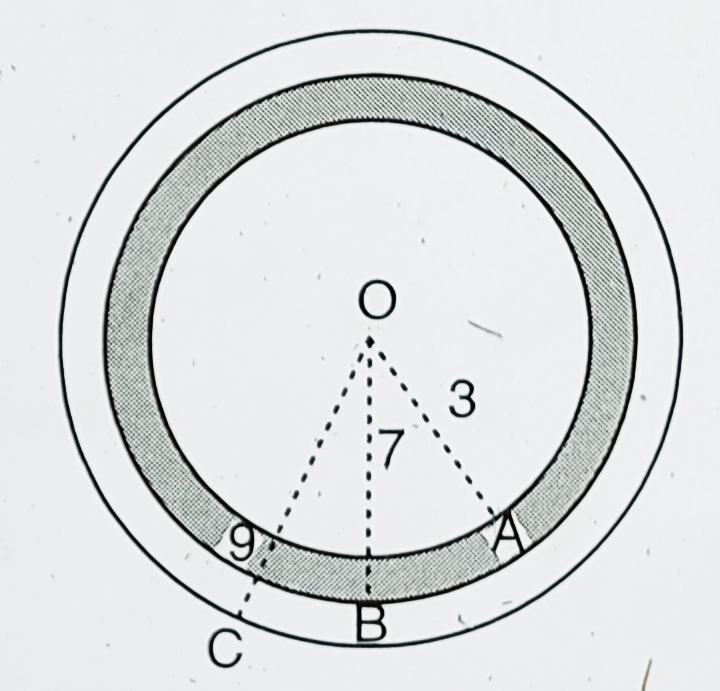
已知:图中所示的目标由三个同心圆组成,其半径分别为 3、7 和 9 厘米。投掷飞镖并落在目标上。求解:我们需要找到飞镖落在阴影区域的概率。解:从图中,$OA=3 cm, OB=7 cm, OC=9 cm$。我们知道,半径为 r 的圆的面积 = $\pi r^2$。半径为 OC 的圆的面积 = $\pi(9)^{2} = 81 \pi$。阴影区域的面积 = $\pi(OB)^{2} - \pi(OA)^{2} = \pi(7)^{2} - \pi(3)^{2} = 49 \pi - 9 \pi = 40 \pi$。因此,飞镖落在阴影区域的概率 = 阅读更多
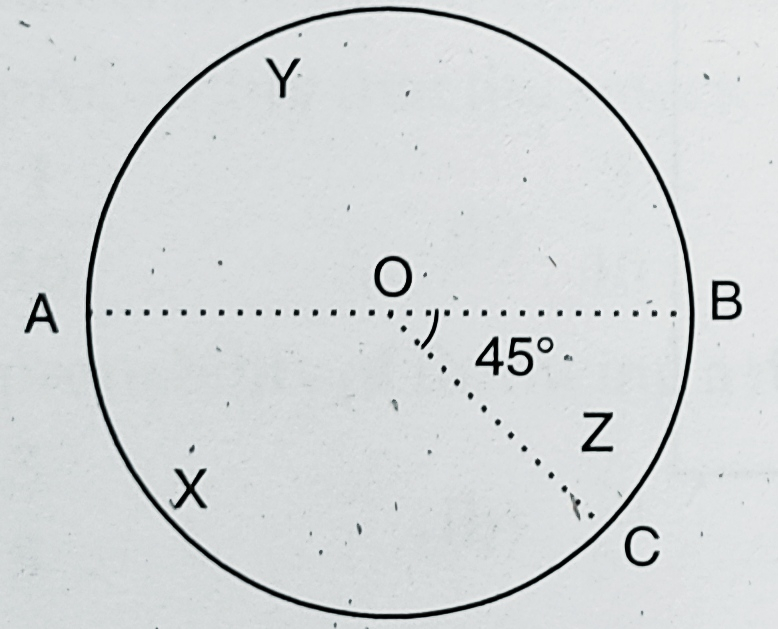
已知:一个公平的旋转器放置在圆的中心 O 处。直径 AOB 和半径 OC 将圆分成三个区域,分别标记为 X、Y 和 Z。$\angle BOC = 45^o$。求解:我们需要找到旋转器落在区域 X 的概率。解:设 r 为圆的半径。$\angle BOC = 45^{\circ}$。X、Y 和 Z 是圆的三个扇形,中心角分别为 $180^{\circ} - 45^{\circ} = 135^{\circ}$、$180^{\circ}$ 和 $45^{\circ}$。因此,旋转器落在区域 X 的概率 = $\frac{X 扇形的面积}{圆的面积} = \frac{\pi r^{2} \times \frac{135^{\circ}}{360^{\circ}}}{\pi r^{2} \times \frac{360^{\circ}}{360^{\circ}}} = \frac{135^{\circ}}{360^{\circ}} = \frac{3}{8}$。旋转器……阅读更多
已知:表达式 (a) 40 = 2 × 2 × 2 × 5 (b) 42 = 7 × 6。 要求:找出进行了质因数分解的表达式。 解:(a) 40 = 2 × 2 × 2 × 5 因为 2 和 5 是质数,所以 40 进行了质因数分解。(b) 42 = 7 × 6 因为 6 不是质数,所以 42 没有进行质因数分解。
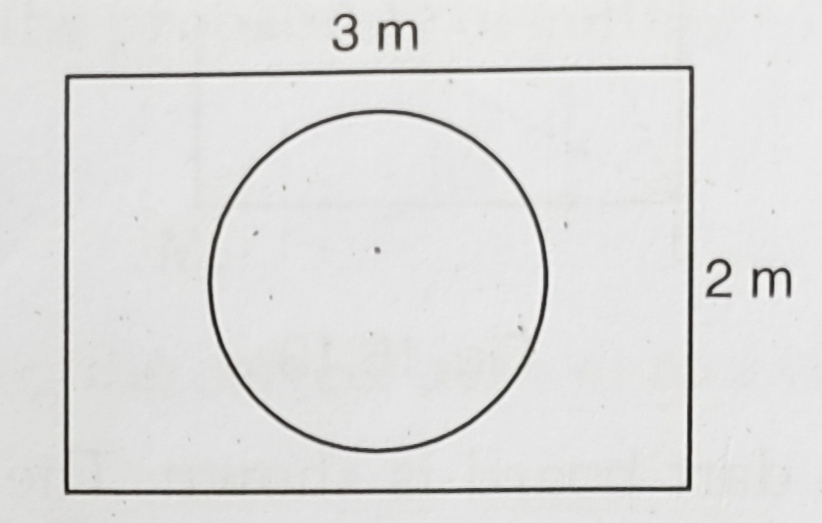
已知:矩形的长 = 3 米,矩形的宽 = 2 米,圆的直径 = 1 米。 要求:我们必须找到领带落在圆内的概率。 解:长为 l,宽为 b 的矩形的面积为 lb。这意味着矩形的面积 = 3 × 2 = 6 平方米。圆的直径 = 1 米,这意味着半径 (r) = 1/2 米。圆的面积 = πr² = π × (1/2)² = π/4 平方米。因此,领带落在圆内的概率 = 圆的面积 / 矩形的面积 = (π/4) / 6 = π / 24 领带落在圆内的概率是 π/24。阅读更多
已知:0.4 ÷ 2。 要求:计算 0.4 ÷ 2。 解:0.4 ÷ 2 = 0.2 因此,0.4 ÷ 2 = 0.2。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP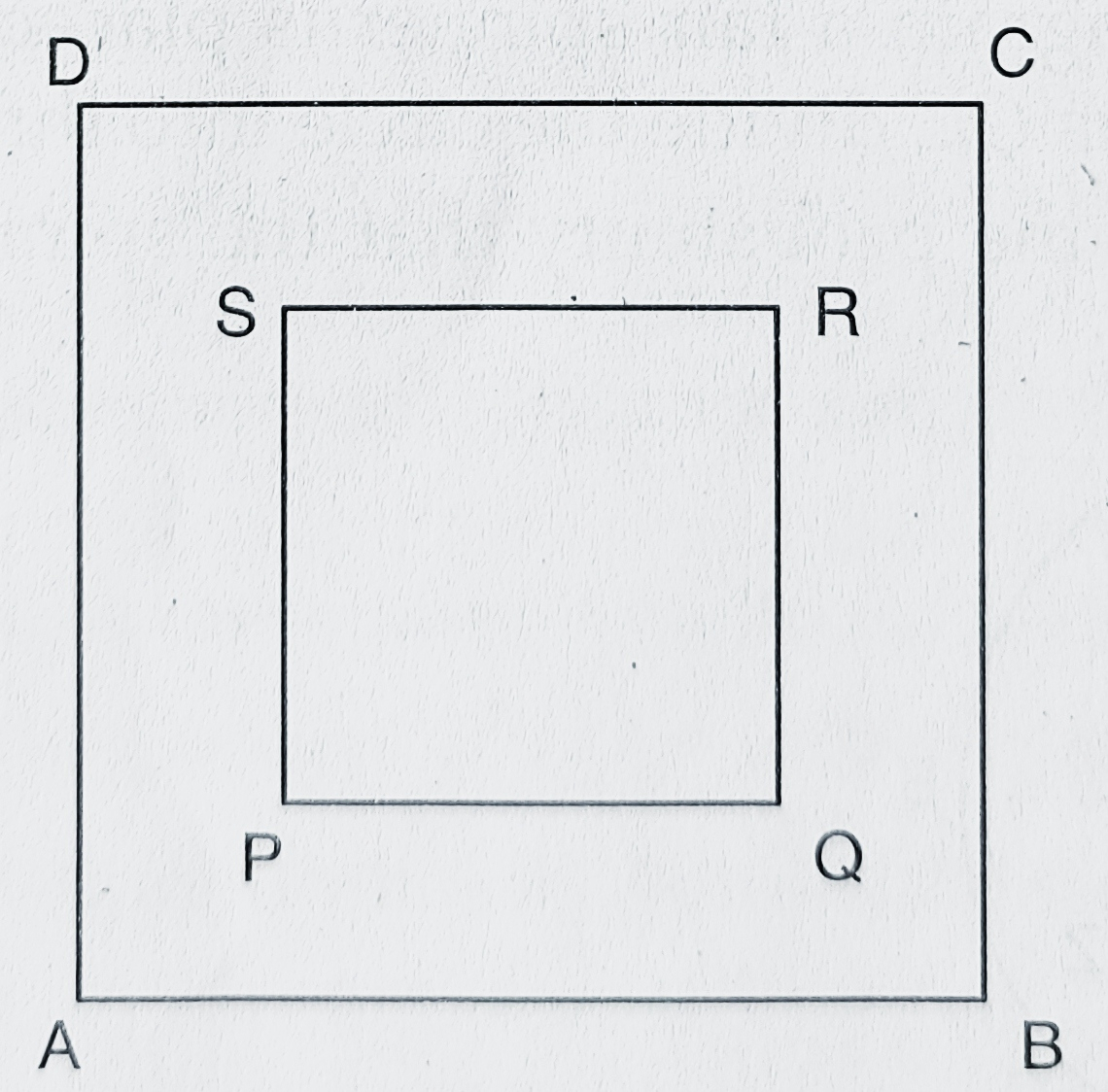 "\
"\
 "\
"\ "\
"\ "\
"\ "\
"\