假设你随机将一条领带掉落在图中所示的矩形区域上。它落在直径为 1 米的圆圈内的概率是多少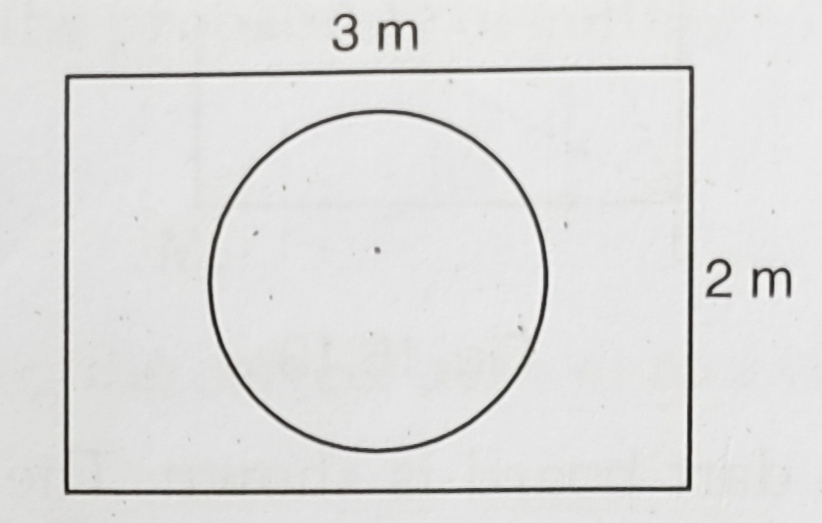？"\n

已知

矩形的长 $=3\ 米$

矩形的宽 $=2\ 米$

圆的直径 $=1\ 米$

要求

我们必须找到领带落在圆圈内的概率。

解答

长为 $l$，宽为 $b$ 的矩形的面积为 $lb$。

这意味着，

矩形的面积 $=3 \times 2=6 \mathrm{~m}^{2}$

圆的直径 $=1 \mathrm{~m}$

这意味着，

半径 $(r)=\frac{1}{2} \mathrm{~m}$

圆的面积 $=\pi r^{2}=\pi \times(\frac{1}{2})^{2}=\frac{1}{4} \pi\ \mathrm{m}^{2}$

因此，

它落在圆圈内的概率 $=\frac{圆的面积}{矩形的面积}$

$=\frac{\frac{1}{4} \pi}{6}$

$=\frac{1 \times \pi}{4 \times 6}$

$=\frac{\pi}{24}$ 

领带落在圆圈内的概率是 $\frac{\pi}{24}$。

教程点

更新于: 2022年10月10日

24 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习