数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学在下图中，一个公平的转盘放置在圆的中心 O 处。直径 AOB 和半径 OC 将圆分成三个区域，分别标记为 X、Y 和 Z。如果∠BOC = 45°，转盘落在区域 X 的概率是多少？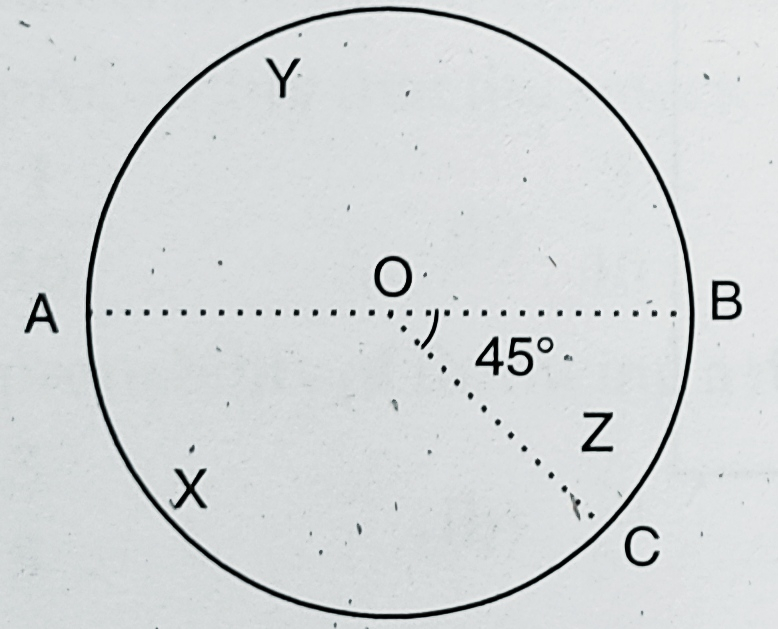
已知
一个公平的转盘放置在圆的中心 O 处。
直径 AOB 和半径 OC 将圆分成三个区域，分别标记为 X、Y 和 Z。
∠BOC = 45°。
要求
我们必须找到转盘落在区域 X 的概率。
解答
设 r 为圆的半径。
∠BOC = 45°
X、Y 和 Z 是圆的三个扇形，其中心角分别为 180° - 45° = 135°、180° 和 45°。
因此，
转盘落在区域 X 的概率 = 扇形 X 的面积 / 圆的面积
= (πr² × 135°/360°) / (πr² × 360°/360°)
= 135°/360°
= 3/8
转盘落在区域 X 的概率是 3/8。
更新于：2022年10月10日
44 次查看
广告