数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究如图所示，JKLM是一个边长为6个单位的正方形。点A和B分别是边KL和LM的中点。如果从正方形内部随机选择一个点，那么该点被选自△JAB内部的概率是多少？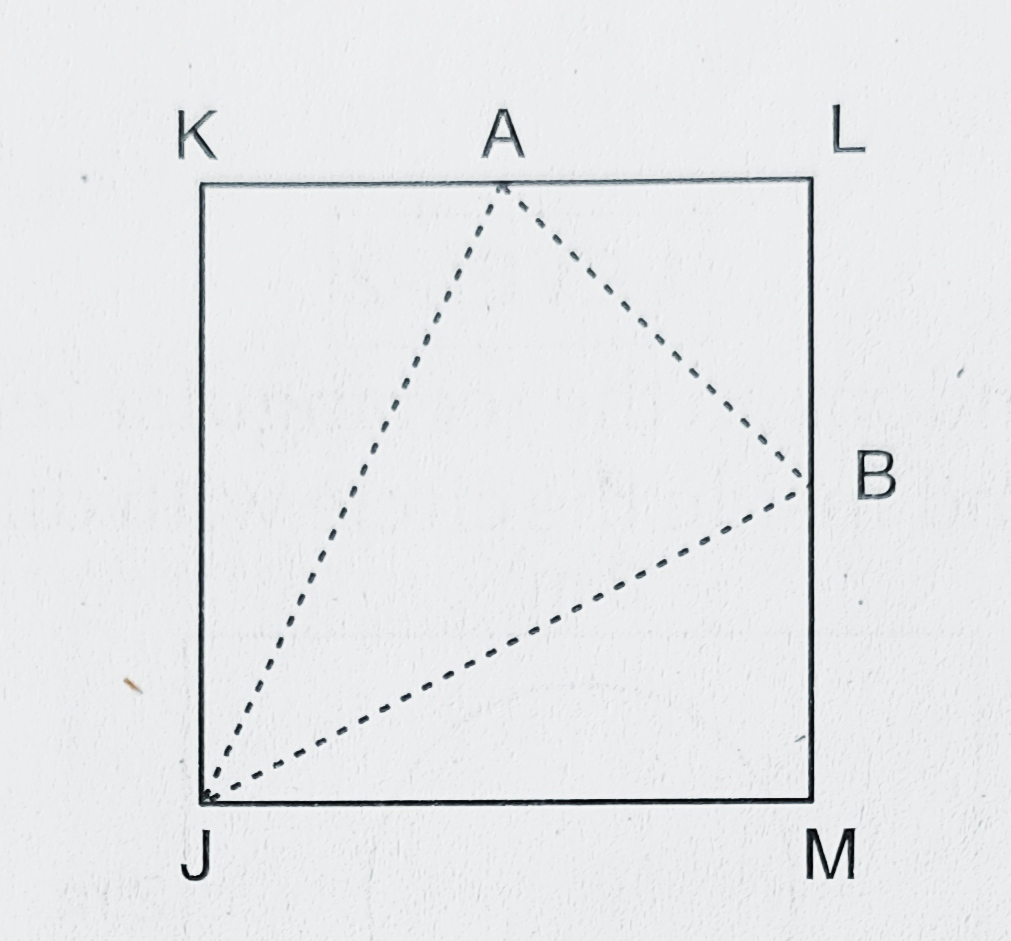
已知
如图所示，JKLM是一个边长为6个单位的正方形。点A和B分别是边KL和LM的中点。
从正方形内部随机选择一个点。
要求
我们必须找到该点被选自△JAB内部的概率。
解答
正方形JKLM的边长 = 6 个单位
正方形的面积 = (6)² = 36 平方单位。
A和B分别是KL和LM边的中点。
AL = AK = BM = BL = 6/2 = 3 个单位
△AJK的面积 = (JK × AK) / 2
=(6 × 3) / 2
= 9 平方单位。
△JMB的面积 = (JM × MB) / 2
=(6 × 3) / 2
= 9 平方单位。
△LAB的面积 = (LA × LB) / 2
=(3 × 3) / 2
= 9/2 平方单位。
三个三角形的面积总和 = 9 + 9 + 9/2
=(18 + 18 + 9) / 2 平方单位
= 45/2 平方单位
因此，
△JAB的面积 = 正方形的面积 - 三个三角形的面积总和
= 36 - 45/2
=(72 - 45) / 2
= 27/2 平方单位
因此，
该点被选自△JAB内部的概率 = △JAB的面积 / 正方形JMLK的面积
=(27/2) / 36
= 3/8
该点被选自△JAB内部的概率是3/8。
更新于：2022年10月10日
浏览量：31
广告