在△ABC中，顶点A的坐标为(0,-1)，D(1,0)和E(0,1)分别是边AB和AC的中点。如果F是边BC的中点，求△DEF的面积。

 已知

在△ABC中，顶点A的坐标为(0,-1)，D(1,0)和E(0,1)分别是边AB和AC的中点。

F是边BC的中点。

要求

我们必须求出△DEF的面积。

解答

设B(x₂，y₂), C(x₃，y₃)是△ABC的另外两个顶点，F(h,k)是BC的中点。

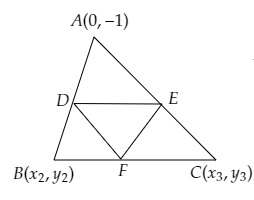
D是AB的中点。

这意味着：

$(\frac{0+x_{2}}{2}, \frac{-1+y_2}{2})=(1,0)$

比较后，我们得到：

$\frac{x_2}{2}=1$ 和 $\frac{-1+y_2}{2}=0$

$x_2=1(2)$ 和 $-1+y_2=0(2)$

$x_2=2$ 和 $y_2=0+1=1$

类似地，

E是AC的中点。

$(\frac{0+x_{3}}{2}, \frac{-1+y_3}{2})=(0,1)$

比较后，我们得到：

$\frac{x_3}{2}=0$ 和 $\frac{-1+y_3}{2}=1$

$x_3=0(2)$ 和 $-1+y_3=1(2)$

$x_3=0$ 和 $y_3=2+1=3$

F是BC的中点。

$(\frac{x_3+x_{2}}{2}, \frac{y_3+y_2}{2})=(h,k)$

比较后，我们得到：

$\frac{2+0}{2}=h$ 和 $\frac{1+3}{2}=k$

$2(h)=2$ 和 $2(k)=4$

$h=1$ 和 $k=2$

我们知道：

顶点为(x₁，y₁)，(x₂，y₂)，(x₃，y₃)的三角形的面积由下式给出：

三角形面积=$\frac{1}{2}[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]$

因此，

三角形DEF的面积=$\frac{1}{2}[1(1-2)+0(2-0)+1(0-1)]$

$=\frac{1}{2}[1(-1)+0+1(-1)]$

$=\frac{1}{2}(-1-1)$

$=\frac{1}{2}(-2)$

$=1$ 平方单位

△DEF的面积是1平方单位。

Tutorialspoint

更新于：2022年10月10日

浏览量：56

开启您的职业生涯

完成课程获得认证

开始学习