数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学如果一个三角形三边的中点坐标分别为$(3, -2), (-3, 1)$和$(4, -3)$，则求其顶点的坐标。
已知
三角形三边的中点坐标为$(3, -2), (-3, 1)$和$(4, -3)$。
求解
我们需要找到三角形的顶点坐标。
解法
设$\triangle ABC$的顶点为$A (x_1, y_1), B (x_2, y_2)$和$C (x_3, y_3)$，$D(3,-2), E(-3,1)$和$F(4,-3)$分别是$BC, CA$和$AB$的中点。
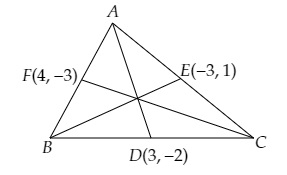
$D$是$BC$的中点。
这意味着：
$\frac{x_{2}+x_{3}}{2}=3$
$\Rightarrow x_{2}+x_{3}=6$ ……(i)
$\frac{y_{2}+y_{3}}{2}=-2$
$\Rightarrow y_{2}+y_{3}=-4$ ……(a)
类似地：
$E$是$AC$的中点。
$\frac{x_{3}+x_{1}}{2}=-3$
$\Rightarrow x_{3}+x_{1}=-6$ ……(ii)
$\frac{y_{3}+y_{1}}{2}=1$
$\Rightarrow y_{3}+y_{1}=2$ ……(b)
$F$是$AB$的中点。
$\frac{x_{2}+x_{1}}{2}=4$
$\Rightarrow x_{2}+x_{1}=8$ ……(iii)
$\frac{y_{2}+y_{1}}{2}=-3$
$\Rightarrow y_{2}+y_{1}=-6$ ……(c)
将(i), (ii)和(iii)相加，得到：
$2(x_{1}+x_{2}+x_{3})=8$
$\Rightarrow x_{1}+x_{2}+x_{3}=4$ ……(iv)
从(iv)中减去(i), (ii)和(iii)，得到：
$x_{1}=-2, x_{2}=10, x_{3}=-4$
类似地：
将(a), (b)和(c)相加，得到：
$2(y_{1}+y_{2}+y_{3})=-8$
$\Rightarrow y_{1}+y_{2}+y_{3}=-4$ ……(d)
从(d)中减去(a), (b)和(c)，得到：
$y_{1}=0, y_{2}=-6, y_{3}=2$
因此，$\triangle ABC$的顶点为$A(-2,0), B(10,-6), C(-4,2)$
三角形的顶点坐标为$(-2,0), (10,-6)$和$(-4,2)$。
41次浏览
