数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学求顶点为(3, 0), (-1, -6)和(4, -1)的三角形外心的坐标及其外接圆半径。
已知
已知点为(3, 0), (-1, -6)和(4, -1)。
要求
我们需要找到三角形外心的坐标及其外接圆半径。
解答
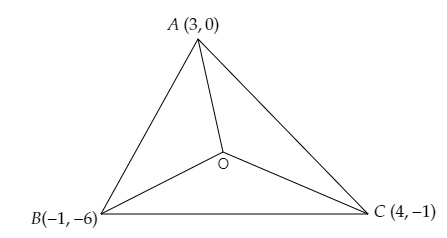
设△ABC的顶点为A(3, 0), B(-1, -6)和C(4, -1)。
设O(x, y)为△ABC的外心。
这意味着：
OA = OB = OC
=> OA² = OB² = OC²
我们知道：
两点A(x₁, y₁)和B(x₂, y₂)之间的距离为√[(x₂-x₁)² + (y₂-y₁)²]。
因此：
OA² = (x-3)² + (y-0)²
= (x-3)² + y²
OB² = (x+1)² + (y+6)²
OC² = (x-4)² + (y+1)²
OA² = OB²
(x-3)² + y² = (x+1)² + (y+6)²
=> x² - 6x + 9 + y² = x² + 2x + 1 + y² + 12y + 36
=> -6x - 2x - 12y = 1 + 36 - 9
=> -8x - 12y = 28
=> 2x + 3y = -7 ……(i)
OB² = OC²
(x+1)² + (y+6)² = (x-4)² + (y+1)²
x² + 2x + 1 + y² + 12y + 36 = x² - 8x + 16 +
y² + 2y + 1
2x + 12y + 37 + 8x - 2y = 17
10x + 10y = 17 - 37 = -20
x + y = -2 ……(ii)
用2乘(ii)式，然后从(i)式中减去，得到：
(2x + 3y) - (2x + 2y) = -7 - (-4)
y = -3
=> x - 3 = -2
=> x = -2 + 3 = 1
O的坐标为(1, -3)。
半径 = OA = √[(1+1)² + (-3+6)²]
= √(2² + 3²)
= √(4 + 9)
= √13 个单位
三角形外心的坐标为(1, -3)，外接圆半径为√13 个单位。
73 次浏览
