求顶点为 $(-2, -3), (-1, 0), (7, -6)$ 的三角形的外心。

已知

已知三角形的顶点为 $(-2, -3), (-1, 0), (7, -6)$。

要求

我们必须找到给定三角形的外心。

解答

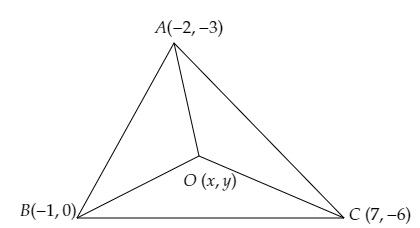
设 $ABC$ 为一个三角形，其顶点为 $A (-2, -3), B (-1, 0)$ 和 $C (7, -6)$。

设 $O(x, y)$ 为 $\Delta A B C$ 的外心。

这意味着，

$\mathrm{OA}=\mathrm{OB}=\mathrm{OC}$

$\Rightarrow \mathrm{OA}^{2}=\mathrm{OB}^{2}=\mathrm{OC}^{2}$

我们知道，

两点 $\mathrm{A}\left(x_{1}, y_{1}\right)$ 和 $\mathrm{B}\left(x_{2}, y_{2}\right)$ 之间的距离为 $\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}$。

因此，

$\mathrm{OA}^{2}=(x+2)^{2}+(y+3)^{2}$

$=x^{2}+4 x+4+y^{2}+6 y+9$

$=x^{2}+y^{2}+4 x+6 y+13$

$\mathrm{OB}^{2}=(x+1)^{2}+(y+0)^{2}$

$=x^{2}+2 x+1+y^{2}$

$=x^{2}+y^{2}+2 x+1$

$\mathrm{OC}^{2}=(x-7)^{2}+(y+6)^{2}$

$=x^{2}-14 x+49+y^{2}+12 y+36$

$=x^{2}+y^{2}-14 x+12 y+85$

$\mathrm{OA}^{2}=\mathrm{OB}^{2}$

$\Rightarrow x^{2}+y^{2}+4 x+6 y+13=x^{2}+y^{2}+2 x+1$

$\Rightarrow  4 x+6 y-2 x=1-13$

$\Rightarrow 2 x+6 y=-12$

$\Rightarrow x+3 y=-6$

$\Rightarrow x=-3y-6$.......(i)
$\mathrm{OB}^{2}=\mathrm{OC}^{2}$

$\Rightarrow x^{2}+y^{2}+2 x+1=x^{2}+y^{2}-14 x+12 y+85$

$\Rightarrow 2 x+14 x-12 y=85-1$
$\Rightarrow 16 x-12 y=84$
$\Rightarrow 4 x-3 y=21$......(ii)
将 $x$ 的值代入 (ii)，得到，

$4(-3 y-6)-3 y=21$

$\Rightarrow -12 y-24-3 y=21$

$\Rightarrow -15 y=21+24$

$\Rightarrow -15 y=45$

$\Rightarrow y=\frac{45}{-15}=-3$

这意味着，

 $x=-3 y-6=-3 \times(-3)-6$

$=9-6=3$
因此，三角形的外心为 $(3,-3)$。

教程点

更新时间： 2022 年 10 月 10 日

835 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习