数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究求顶点坐标为$(-3, 2), (5, 4), (7, -6)$ 和 $(-5, -4)$ 的四边形的面积。
已知
四边形的顶点为$(-3, 2), (5, 4), (7, -6)$ 和 $(-5, -4)$。
要求
我们需要求出四边形的面积。
解法
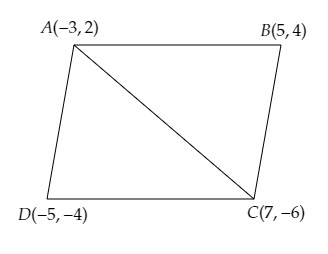
设$A(-3, 2), B(5, 4), C(7, -6)$ 和 $D(-5, -4)$ 为四边形$ABCD$ 的顶点。
连接$A$ 和 $C$，得到两个三角形$ABC$ 和 $ADC$。
这意味着：
四边形$ABCD$ 的面积 = 三角形$ABC$ 的面积 + 三角形$ADC$ 的面积。
我们知道：
顶点为$(x_1,y_1), (x_2,y_2), (x_3,y_3)$ 的三角形的面积由下式给出：
三角形面积$\Delta=\frac{1}{2}[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]$
因此：
三角形\( ABC\) 的面积\(=\frac{1}{2}[-3(4+6)+5(-6-2)+7(2-4)] \)
\( =\frac{1}{2}[-3(10)+5(-8)+7(-2)] \)
\( =\frac{1}{2}[-30-40-14] \)
\( =\frac{1}{2} \times (-84) \)
\( =42 \) 平方单位。
三角形\( ADC\) 的面积\(=\frac{1}{2}[-3(-6+4)+7(-4-2)+-5(2+6)] \)
\( =\frac{1}{2}[-3(-2)+7(-6)+(-5)(8)] \)
\( =\frac{1}{2}[6-42-40] \)
\( =\frac{1}{2} \times (-76) \)
\( =38 \) 平方单位。
因此：
四边形$ABCD$ 的面积 = $42 + 38 = 80$ 平方单位。
给定四边形的面积为 80 平方单位。
浏览量：58
