一个四边形的四个顶点按顺序为$(1, 2), (-5, 6), (7, -4)$ 和 $(k, -2)$。如果四边形的面积为零，求 $k$ 的值。

已知

一个四边形的四个顶点按顺序为 $(1, 2), (-5, 6), (7, -4)$ 和 $(k, -2)$。

四边形的面积为零。

要求

我们需要求出 $k$ 的值。

解答

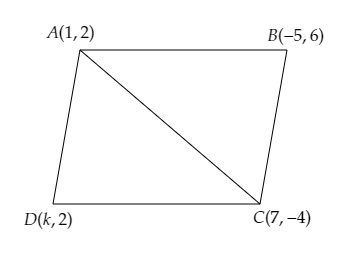
设 $A(1, 2), B(-5, 6), C(7, -4)$ 和 $D(k, -2)$ 为四边形 $ABCD$ 的顶点。

连接 $A$ 和 $C$，得到两个三角形 $ABC$ 和 $ADC$。

这意味着：

四边形 $ABCD$ 的面积 = 三角形 $ABC$ 的面积 + 三角形 $ADC$ 的面积。

我们知道：

顶点为 $(x_1, y_1), (x_2, y_2), (x_3, y_3)$ 的三角形的面积由下式给出：

三角形面积 $\Delta=\frac{1}{2}[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]$

因此：

三角形 $ABC$ 的面积 $= \frac{1}{2}[1(6+4)+(-5)(-4-2)+7(2-6)]$

$= \frac{1}{2}[1(10)+(-5)(-6)+7(-4)]$

$= \frac{1}{2}[10+30-28]$

$= \frac{1}{2} \times 12$

$= 6$ 平方单位。

三角形 $ADC$ 的面积 $= \frac{1}{2}[1(-4+2)+k(2+4)+7(-2-2)]$

$= \frac{1}{2}[1(-2)+k(6)+7(-4)]$

$= \frac{1}{2}[-2+6k-28]$

$= \frac{1}{2}(6k-30)$

$= 3k-15$ 平方单位。

因此：

四边形 $ABCD$ 的面积 $= 6 + 3k - 15$ 平方单位。

$0 = 3k - 9$

$3k = 9$

$k = \frac{9}{3}$

$k = 3$

$k$ 的值为 $3$。

教程点

更新于：2022年10月10日

111 次浏览

开启你的职业生涯

完成课程获得认证

开始学习