\( \mathrm{ABC} \)是一个三角形。在\( \triangle \mathrm{ABC} \)的内部找到一个与\( \triangle \mathrm{ABC} \)所有顶点等距的点。

已知
 $ABC$是一个三角形。

任务

我们必须在$\triangle ABC$的内部找到一个与$\triangle ABC$所有顶点等距的点。

解答

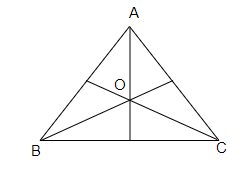
让我们考虑一个$\triangle ABC$

我们知道，

三角形内部与所有顶点等距的点称为三角形的圆心。

我们也知道，

三角形的圆心是三角形所有边的垂直平分线相交的点。

因此，

在$\triangle ABC$中，让我们从点$A$、$B$和$C$画三条垂直平分线，

让我们将交点标记为点$O$

因此，$O$是$\triangle ABC$内部所需的点，它与$\triangle ABC$的所有顶点等距。

教程点

更新于：2022年10月10日

54 次浏览

开启您的职业生涯

完成课程获得认证

开始学习