Tutorialspoint

更新于 2022年10月10日 10:54:12

157 次浏览

 (a) 这些镜片中间较厚，因为它们的屈光度为正，这意味着它们是凸透镜。(b) 左眼的镜片对光线的弯曲程度更大，因为它焦距较短。我们知道，屈光度与焦距成反比 ($P=\frac {1}{f}$)。因此，屈光度更大的镜片焦距较短，在本例中为 +2.50D。(c) 这些眼镜会使光线会聚，因为它们是凸透镜。

Tutorialspoint

更新于 2022年10月10日 10:54:12

38 次浏览

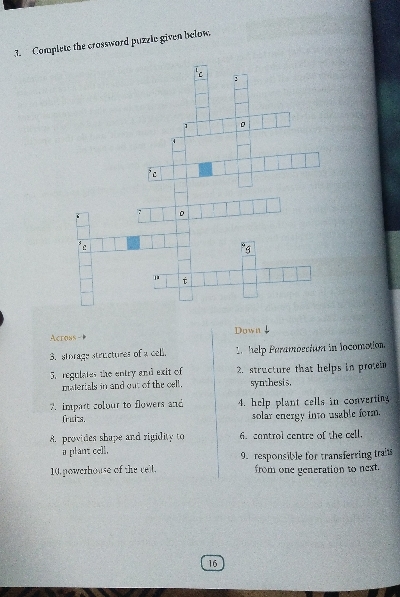
1. 纤毛：帮助草履虫运动。2. 核糖体：帮助蛋白质合成的结构。3. 液泡：细胞的储存结构。4. 叶绿体：帮助植物细胞将太阳能转化为可用形式。5. 细胞膜：调节物质进出细胞。6. 细胞核：细胞的控制中心。7. 染色体：赋予花朵和果实颜色。8. 细胞壁：赋予植物细胞形状和坚硬度。9. 基因：负责将性状从一代传递到下一代。10. 线粒体：细胞的动力源。

Tutorialspoint

更新于 2022年10月10日 10:54:10

31 次浏览

解题步骤：我们需要绘制累积频数曲线来表示给定的频数分布。解：给定的频数分布不是连续的。所以，我们首先将其变为连续的，并准备如下所示的累积频数分布：在X轴上表示组距，在Y轴上表示累积频数。在图上绘制点 (4.5, 2), (9.5, 8), (14.5, 18), (19.5, 23) 和 (24.5, 26)，并用自由手绘线连接它们，得到如图所示的累积频数曲线。这就是所需的累积频数曲线。

Tutorialspoint

更新于 2022年10月10日 10:54:09

54 次浏览

已知：750 名学生在考试中取得的分数以频数分布表的形式给出。解题步骤：我们需要用“小于”方法准备累积频数表并绘制累积频数曲线。解：我们首先准备如下所示的“小于”方法的累积频数分布表：在X轴上取分数，在Y轴上取学生人数（累积频数）。在图上绘制点 (640, 16), (680, 61), (720, 217), (760, 501), (800, 673), (840, 732) 和 (880, 750)，并用自由手绘线连接它们。这就是所需的“小于”累积频数曲线。

Tutorialspoint

更新于 2022年10月10日 10:54:07

45 次浏览

已知：给定的分布显示了一些世界顶级击球手在一场日国际板球比赛中取得的总得分。解题步骤：我们需要求数据的众数。解：给定数据的频数如下所示。得分（$x_i$）：击球手人数（$f_i$）：3000-4000 4 4000-5000 18 5000-6000 9 6000-7000 7 7000-8000 6 8000-9000 3 9000-10000 1 10000-11000 1 我们观察到 4000-5000 组的频数最大（18）。因此，它是众数组。这里，$l=4000, h=1000, f=18, f_1=4, f_2=9$ 我们知道，众数 $=l+\frac{f-f_1}{2 f-f_1-f_2} \times h$$=4000+\frac{18-4}{2 \times 18-4-9} \times 1000$$=4000+\frac{14}{36-13} \times1000$$=4000+\frac{14000}{23}$$=4000+608.7$$=4608.7$ 给定数据的众数是 4608.7。阅读更多

Tutorialspoint

更新于 2022年10月10日 10:54:07

93 次浏览

已知：给出了一个村庄农业用地持有的频数分布表。解题步骤：我们需要求该村庄农业用地持有的众数。解：给定数据的频数如下所示。土地面积（公顷）（$x_i$）：家庭数量（$f_i$）：1-3 20 3-5 45 5-7 80 7-9 55 9-11 40 11-13 12 我们观察到 5-7 组的频数最大（80）。因此，它是众数组。这里，$l=5, h=2, f=80, f_1=45, f_2=55$ 我们知道，众数 $=l+\frac{f-f_1}{2 f-f_1-f_2} \times h$$=5+\frac{80-45}{2 \times 80-45-55} \times 2$$=5+\frac{35}{160-100} \times2$$=5+\frac{70}{60}$$=5+1.16$$=6.16$ 该村庄农业用地持有的众数是 6.2 公顷。阅读更多

Tutorialspoint

更新于 2022年10月10日 10:54:07

61 次浏览

已知：给出了 100 个家庭的月收入。解题步骤：我们需要求众数收入。解：给定数据的频数如下所示。收入（人民币）（$x_i$）：家庭数量（$f_i$）：0-5000 8 5000-10000 26 10000-15000 41 15000-20000 16 20000-25000 3 25000-30000 3 30000-35000 2 35000-40000 1 我们观察到 10000-15000 组的频数最大（41）。因此，它是众数组。这里，$l=10000, h=5000, f=41, f_1=26, f_2=16$ 我们知道，众数 $=l+\frac{f-f_1}{2 f-f_1-f_2} \times h$$=10000+\frac{41-26}{2 \times 41-26-16} \times 5000$$=10000+\frac{15}{82-42} \times5000$$=10000+\frac{75000}{40}$$=10000+1875$$=11875$ 众数收入是人民币 11875 元。

Tutorialspoint

更新于 2022年10月10日 10:54:07

49 次浏览

解题步骤：我们需要根据给定的数据绘制“小于”方法的累积频数曲线。解：我们首先准备如下所示的“小于”方法的累积频数分布表：在X轴上取房间数量，在Y轴上取累积频数。在图上绘制点 (1, 4), (2, 13), (3, 35), (4, 63), (5, 87), (6, 99), (7, 107), (8, 113), (9, 118) 和 (10, 120)，并用自由手绘线连接它们，得到如图所示的累积频数曲线。这就是所需的“小于”累积频数曲线。

Tutorialspoint

更新于 2022年10月10日 10:54:06

66 次浏览

已知：给定数据显示了某村200户家庭每月总支出的分布情况。任务：我们必须找到家庭的众数月支出和平均月支出。解答：给定数据的频率如下所示。我们知道，设假设平均值为$A=2750$。平均值 $=A+h \times \frac{\sum{f_iu_i}}{\sum{f_i}}$因此，平均值 $=2750+500\times(\frac{-35}{200})$ $=2750-2.5\times35$ $=2750-87.5$ $=2662.5$给定数据的平均值为2662.50元。我们观察到，1500-2000的区间频率最高(40)。因此，它是众数区间。这里，$l=1500, h=500, f=40, f_1=24, f_2=33$我们知道，众数 $=l+\frac{f-f_1}{2 f-f_1-f_2} \times h$ $=1500+\frac{40-24}{2 \times 40-24-33} \times 500$ $=1500+\frac{16}{80-57} \times 500$ $=1500+\frac{8000}{23}$ $=1500+347.83$ $=1847.83$众数...阅读更多

Tutorialspoint

更新于 2022年10月10日 10:54:05

浏览量 173

任务：我们必须找到下列数据的平均数、中位数和众数。解答：给定数据的频率如下所示。设假设平均值为$A=70$。我们知道，平均值 $=A+\frac{\sum{f_id_i}}{\sum{f_i}}$因此，平均值 $=70+(\frac{-380}{50})$ $=70-7.6$ $=62.4$给定数据的平均值为62.4。我们观察到，60-80的区间频率最高(12)。因此，它是众数区间。这里，$l=60, h=20, f=12, f_1=10, f_2=6$我们知道，众数 $=l+\frac{f-f_1}{2 f-f_1-f_2} \times h$ $=60+\frac{12-10}{2 \times 12-10-6} \times 20$ $=60+\frac{2}{24-16} \times 20$ $=60+\frac{40}{8}$ $=60+5$ $=65$给定数据的众数为65。这里，$N=50$这意味着，$\frac{N}{2}=\frac{50}{2}=25$中位数区间 $=60-80$我们知道，中位数 $=l+\frac{\frac{N}{2}-F}{f} \times h$ $=60+\frac{25-24}{12} \times 20$ $=60+\frac{20}{12}$ $=60+1.66=61.66$给定数据的...阅读更多