(i) 光线图 -(ii) 所形成图像的两个特征是:1. 它是虚像且正立的。(镜后且直立)2. 它比物体小。(iii) 给定:凸面镜物体距离,$u$ = $-$10 cm镜面焦距,$f$ = 5 cm需计算:图像到镜面的距离,$v$。解:根据镜面公式,我们知道-$\frac {1}{f}=\frac {1}{v}+\frac {1}{u}$代入给定值,得到-$\frac {1}{5}=\frac {1}{v}+\frac {1}{(-10)}$$\frac {1}{5}=\frac {1}{v}-\frac {1}{10}$ $\frac {1}{5}+\frac {1}{10}=\frac {1}{v}$$\frac {1}{v}=\frac {2+1}{10}$$\frac {1}{v}=\frac {3}{10}$$v=\frac {10}{3}$ $v=+0.3cm$ 因此,图像的距离 $v$ 为 0.3 cm,距镜面,并且 ... 阅读更多
给定:$\frac{-16}{23} \times \frac{47}{-288} \times \frac{92}{-141}$。需要做:将 $\frac{-16}{23} \times \frac{47}{-288} \times \frac{92}{-141}$ 写成简化形式。解:$\frac{-16}{23} \times \frac{47}{-288} \times \frac{92}{-141}$$=\frac{-16}{23} \times \frac{47}{-16\times 18} \times \frac{23\times4}{-47\times3}$$=-\frac{4}{54}$
给定:数字 $15,\ 45,\ 40,\ 120$。需要做:确定 $15,\ 45,\ 40,\ 120$ 的比例。解:我们有 $15,\ 45,\ 40,\ 120$。因此,$15$ 和 $45$ 的比率为 $\frac{15}{45}=\frac{1}{3}=1:3$ $40$ 和 $120$ 的比率为 $\frac{40}{120}=\frac{1}{3}=1:3$ 因此,$15:45::40:120$。
给定:一个风筝的形状为正方形,对角线为 $32\ cm$,一个等腰三角形的底为 $8\ cm$,两边各为 $6\ cm$,需要用三种不同的颜色制作,如图所示。需要做:找出每种颜色使用了多少纸?解:假设风筝是由正方形 $ABCD$ 和等腰 $\vartriangle DEF$ 组成的。给定,$\vartriangle DEF$ 的边长为 $DE=DF=6\ cm$ 和 $EF=8\ cm$,正方形 $ABCD$ 的对角线为 $32\ cm$。我们知道,正方形的对角线互相垂直平分。$OA=OB=OC=OD=\frac{32}{2}=16\ cm$$AO$ 垂直 ... 阅读更多
给定:\( A \) 和 \( B \) 是锐角,使得 \( \tan A=\frac{1}{2}, \tan B=\frac{1}{3} \) 且 \( \tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B} \)。需要做:我们必须找到 \( A+B \)。解: \( \tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B} \)这意味着,\( \tan (A+B)=\frac{\frac{1}{2}+\frac{1}{3}}{1-(\frac{1}{2})(\frac{1}{3})} \) \( =\frac{\frac{1(3)+1(2)}{6}}{1-(\frac{1}{6})} \)\( =\frac{\frac{3+2}{6}}{\frac{1(6)-1}{6}} \)\( =\frac{5}{5} \)\( =1 \)\( \Rightarrow \tan (A+B)=\tan 45^{\circ} \) (因为 $\tan 45^o=1$)因此,$A+B$ 的值为 $45^{\circ}$。
需要做:我们必须证明 \( (\sqrt{3}+1)(3-\cot 30^{\circ})=\tan^{3} 60^{\circ}-2\sin 60^{\circ} \)。解: 我们知道,$\cot 30^{\circ}=\sqrt3$$\tan 60^{\circ}=\sqrt3$$\sin 60^{\circ}=\frac{\sqrt3}{2}$让我们考虑 LHS,$(\sqrt{3}+1)(3-\cot 30^{\circ})=(\sqrt{3}+1)(3-\sqrt3)$$=(\sqrt{3})(3)-(\sqrt3)^2+1(3)-1(\sqrt3)$$=3\sqrt3-3+3-\sqrt3$$=2\sqrt3$ 让我们考虑 RHS,$\tan^{3} 60^{\circ}-2\sin 60^{\circ}=(\sqrt3)^3-2(\frac{\sqrt3}{2})$$=3\sqrt3-\sqrt3$$=2\sqrt3$LHS $=$ RHS因此得证。
给定:\( \frac{\sin 20^{\circ}}{\cos 70^{\circ}} \)需要做:我们必须计算 \( \frac{\sin 20^{\circ}}{\cos 70^{\circ}} \)。解: 我们知道,$cos\ (90^{\circ}- \theta) = sin\ \theta$因此,$\frac{\sin 20^{\circ}}{\cos 70^{\circ}}=\frac{\sin 20^{\circ}}{\cos (90^{\circ}-20^{\circ})}$$=\frac{\sin 20^{\circ}}{\sin 20^{\circ}}$$=1$因此,$\frac{\sin 20^{\circ}}{\cos 70^{\circ}}=1$。
给定:\( \frac{\cos 19^{\circ}}{\sin 71^{\circ}} \)需要做:我们必须计算 \( \frac{\cos 19^{\circ}}{\sin 71^{\circ}} \)解: 我们知道,$sin\ (90^{\circ}- \theta) = cos\ \theta$因此,$\frac{\cos 19^{\circ}}{\sin 71^{\circ}}=\frac{\cos 19^{\circ}}{\sin (90^{\circ}-19^{\circ})}$$=\frac{\cos 19^{\circ}}{\cos 19^{\circ}}$$=1$因此,$\frac{\cos 19^{\circ}}{\sin 71^{\circ}}=1$。
已知:\( \frac{\sin 21^{\circ}}{\cos 69^{\circ}} \)要求:我们需要计算 \( \frac{\sin 21^{\circ}}{\cos 69^{\circ}} \)的值。解:我们知道,$cos\ (90^{\circ}- \theta) = sin\ \theta$因此,$\frac{\sin 21^{\circ}}{\cos 69^{\circ}}=\frac{\sin 21^{\circ}}{\cos (90^{\circ}-21^{\circ})}$$=\frac{\sin 21^{\circ}}{\sin 21^{\circ}}$$=1$因此,$\frac{\sin 21^{\circ}}{\cos 69^{\circ}}=1$。

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
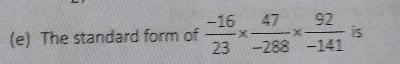 "\
"\ "\
"\