数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：四边形的顶点为 $(-3, 2), (5, 4), (7, -6)$ 和 $(-5, -4)$。要求：我们需要求出四边形的面积。解：设 $A(-3, 2), B(5, 4), C(7, -6)$ 和 $D(-5, -4)$ 是四边形 $ABCD$ 的顶点。连接 $A$ 和 $C$ 得到两个三角形 $ABC$ 和 $ADC$。这意味着，四边形 $ABCD$ 的面积 = 三角形 $ABC$ 的面积 + 三角形 $ADC$ 的面积。我们知道，顶点为 $(x_1, y_1), (x_2, y_2), (x_3, y_3)$ 的三角形的面积由下式给出：三角形面积 = $\frac{1}{2}[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]$因此，三角形 \( ABC\) 的面积 = $\frac{1}{2}[-3(4+6)+5(-6-2)+7(2-4)]$ \( =\frac{1}{2}[-3(10)+5(-8)+7(-2)] \)\( =\frac{1}{2}[-30-40-14] \)\( =\frac{1}{2} \times (-84) \)\( =42 \) 平方单位。面积 ... 阅读更多
已知：$G$ 是三角形 ABC 的重心。要求：我们需要证明 $AB^2 + BC^2 + CA^2 = 3 (GA^2 + GB^2 + GC^2)$。解：设三角形 $\triangle ABC$ 顶点的坐标为 $A (x_1, y_1), B (x_2, y_2), C (x_3, y_3)$，且 $G$ 为三角形的重心。因此，\( \mathrm{G} \) 的坐标为 让我们考虑 LHS， \( A B^{2}+B C^{2}+C A^{2}=\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}+\left(x_{2}-x_{3}\right)^{2}+\left(y_{2}-y_{3}\right)^{2}+\left(x_{3}-x_{1}\right)^{2}+\left(y_{3}-y_{1}\right)^{2} \)\( =\left(x_{1}-x_{2}\right)^{2}+\left(x_{2}-x_{3}\right)^{2}+\left(x_{3}-x_{1}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}+\left(y_{2}-y_{3}\right)^{2}+\left(y_{3}-y_{1}\right)^{2} \)\( =x_{1}^{2}+x_{2}^{2}-2 x_{1} x_{2}+x_{2}^{2}+x_{3}^{2}-2 x_{2} x_{3}+x_{3}^{2}+x_{1}^{2}-2 x_{3} x_{1}+y_{1}^{2}+y_{2}^{2}-2 y y_{2}+y_{2}^{2}+y_{3}^{2}-2 y_{2} y_{3}+y_{3}^{2} +y_{1}^{2}-2 y y \)\( =2\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\right)-2\left(x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}\right)+2\left(y_{1}^{2}+y_{2}^{2}+y_{3}^{2}\right)-2\left(y_{1} y_{2}+y_{2} y_{3}+y_{3} y_{1}\right) \)现在，让我们考虑 RHS， \( 3\left[\mathrm{GA}^{2}+\mathrm{GB}^{2}+\mathrm{GC}^{2}\right] \)\( =3\left[\begin{array}{l}\left.\left(x_{1}-\frac{x_{1}+x_{2}+x_{3}}{3}\right)^{2}+\left(y_{1}-\frac{y_{1}+y_{2}+y_{3}}{3}\right)^{2}+\left(x_{2}-\frac{x_{1}+x_{2}+x_{3}}{3}\right)^{2}+\left(y_{2}-\frac{y_{1}+y_{2}+y_{3}}{3}\right)^{2}\right] ... 阅读更多
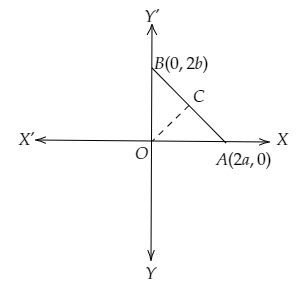
"\已知：给定一个直角三角形 BOA。$C$ 是斜边 AB 的中点。要求：我们需要证明 $C$ 与顶点 $O, A$ 和 $B$ 等距。解：在 $\triangle OAB$ 中，$O$ 的坐标为 $(0, 0)$，$A$ 的坐标为 $(2a, 0)$，$B$ 的坐标为 $(0, 2b)$。$C$ 是 $AB$ 的中点。使用中点公式，我们得到，$C$ 的坐标为 \( \left(\frac{2 a+0}{2}, \frac{0+2 b}{2}\right) \)\( =(a, b) \)\( \mathrm{CO}=\sqrt{(a+0)^{2}+(b+0)^{2}} \)\( =\sqrt{a^{2}+b^{2}} \)使用距离公式，我们得到， \( \mathrm{CA}=\sqrt{(2 a-a)^{2}+(0-b)^{2}} \)\( =\sqrt{(a)^{2}+(b)^{2}} \)\( =\sqrt{a^{2}+b^{2}} \)\( \mathrm{CB}=\sqrt{(0-a)^{2}+(2 b-b)^{2}} \)\( =\sqrt{(-a)^{2}+(b)^{2}} \)\( =\sqrt{a^{2}+b^{2}} \)这里，$CO = CA = CB$这意味着，$C$ 是 ... 阅读更多
要求：我们需要证明连接四边形对边中点的线段与连接其对角线中点的线段相交于一点，且互相平分。解：设 $A (x_1, y_1), B (x_2, y_2), C (x_3, y_3)$ 和 $D (x_4, y_4)$ 是四边形 $ABCD$ 的顶点。$E$ 和 $F$ 分别是边 $BC$ 和 $AD$ 的中点。$G$ 和 $H$ 分别是对角线 $AC$ 和 $BD$ 的中点。这意味着，\( \mathrm{E} \) 的坐标为 \( (\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2}) \)F 的坐标为 \( (\frac{x_{1}+x_{4}}{2}, \frac{y_{1}+y_{4}}{2}) \) ... 阅读更多
已知：$G$ 是三角形 ABC 的重心，而 $P$ 是平面上的任意一点。要求：我们需要证明 $PA^2 + PB^2 + PC^2 = GA^2 + GB^2 + GC^2 + 3GP^2$。解：设 $G(u, v)$ 是 $\triangle ABC$ 的重心，$A$ 的坐标为 $(x_1, y_1)$，$B$ 的坐标为 $(x_2, y_2)$，$C$ 的坐标为 $(x_3, y_3)$。设 $P (h, k)$ 是平面上的任意一点。重心 \( \mathrm{G} \) 的坐标为 \( (\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}) \)这意味着， \( u=\frac{x_{1}+x_{2}+x_{3}}{3} \) 和 \( v=\frac{y_{1}+y_{2}+y_{3}}{3} \)让我们考虑 LHS， \( \mathrm{PA}^{2}+\mathrm{PB}^{2}+\mathrm{PC}^{2}=\left(h-x_{1}\right)^{2}+\left(k-y_{1}\right)^{2}+\left(h-x_{2}\right)^{2}+\left(k-y_{2}\right)^{2}+\left(h-x_{3}\right)^{2}+\left(k-y_{3}\right)^{2} \)\( = 3\left(h^{2}+k^{2}\right)+\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\right)+\left(y_{1}^{2}+y_{2}^{2}+y_{3}^{2}\right)-2 h\left(x_{1}+x_{2}+x_{3}\right)-2 k\left(y_{1}+y_{2}+y_{3}\right) \)\( =\left(3 h^{2}+k^{2}\right)+\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\right)+\left(y_{1}^{2}+y_{2}^{2}+y_{3}^{2}\right)-2 ... 阅读更多
要求：我们需要证明三角形两边中点连线等于第三边的一半。解：设 $A(x_1, y_1), B(x_2, y_2), C(x_3, y_3)$ 是 $\triangle ABC$ 的顶点。设 $D$ 和 $E$ 分别是边 $AB$ 和 $AC$ 的中点。这意味着， \( \mathrm{DE}=\frac{1}{2} \mathrm{BC} \) \( \mathrm{D} \) 的坐标为 \( \left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right) \) \( \mathrm{E} \) 的坐标为 \( \left(\frac{x_{1}+x_{3}}{2}, \frac{y_{1}+y_{3}}{2}\right) \) 边 $BC$ 的长度 = $\sqrt{(x_3-x_2)^2+(y_3-y_2)^2}$......(i) 边 $DE$ 的长度 = $\sqrt{\left(\frac{x_{1} +x_{3}}{2} -\frac{x_{1} +x_{2}}{2}\right)^{2} +\left(\frac{y_{1} +y_{3}}{2} -\frac{y_{1} +y_{3}}{2}\right)^{2}}$$=\sqrt{\frac{(x_1+x_3-x_1-x_2)^2}{4}+\frac{(y_1+y_3-y_1-y_2)^2}{4}}$$=\sqrt{\frac{( ... 阅读更多
已知：点 $A (x_1, y_1), B (x_2, y_2)$ 和 $C (x_3, y_3)$ 是 $\triangle ABC$ 的顶点。$AP : PD = 2 : 1$。求解：我们必须找到点 $P$ 在 $AD$ 上的坐标。解：$D$ 是 $BC$ 的中点。这意味着，使用中点公式，我们得到，$D$ 的坐标为 $(\frac{x_2+x_3}{2}, \frac{y_2+y_3}{2})$。$AP : PD = 2 : 1$。使用截距公式，我们得到，\( (x, y)=(\frac{m x_{2}+n x_{1}}{m+n}, \frac{m y_{2}+n y_{1}}{m+n}) \)点 \( \mathrm{P} \) 的坐标为 \( (\frac{2 \times \frac{x_2+x_3}{2}+1 \times x_1}{1+2}, \frac{2 \times \frac{y_2+y_3}{2}+1 \times y_1}{1+2}) \)\( =(\frac{x_2+x_3+x_1}{3}, \frac{y_2+y_3+y_1}{3}) \)\( =(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}) \) 点 \( \mathrm{P} \) 的坐标为 \( (\frac{x_1+x_2+x_3}{3}, ... 阅读更多
已知：点 $A (x_1, y_1), B (x_2, y_2)$ 和 $C (x_3, y_3)$ 是 $\triangle ABC$ 的顶点。$BQ : QE = 2 : 1$ 且 $CR : RF = 2 : 1$。求解：我们必须找到分别在中线 $BE$ 和 $CF$ 上的点 $Q$ 和 $R$ 的坐标。解：$D$ 是 $BC$ 的中点。这意味着，使用中点公式，我们得到，$D$ 的坐标为 $(\frac{x_2+x_3}{2}, \frac{y_2+y_3}{2})$。$AP : PD = 2 : 1$。使用截距公式，我们得到，\( (x, y)=(\frac{m x_{2}+n x_{1}}{m+n}, \frac{m y_{2}+n y_{1}}{m+n}) \)点 \( \mathrm{P} \) 的坐标为 \( (\frac{2 \times \frac{x_2+x_3}{2}+1 \times x_1}{1+2}, \frac{2 \times \frac{y_2+y_3}{2}+1 \times ... 阅读更多
已知：点 $A (x_1, y_1), B (x_2, y_2)$ 和 $C (x_3, y_3)$ 是 $\triangle ABC$ 的顶点。求解：我们必须找到三角形 ABC 的重心的坐标。解：我们知道，三角形重心的坐标为 $(\frac{横坐标之和}{3}, \frac{纵坐标之和}{3})$因此，三角形 ABC 的重心的坐标为，$(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3})$三角形 ABC 的重心的坐标为 $(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3})$。
已知：点 $(1, 4), (-1, -1), (3, -2)$ 是三角形的顶点。求解：我们必须找到给定三角形的重心。解：我们知道，三角形重心的坐标为 $(\frac{横坐标之和}{3}, \frac{纵坐标之和}{3})$因此，给定三角形的重心的坐标为，$(\frac{1+(-1)+3}{3}, \frac{4+(-1)+(-2)}{3})$$=(\frac{3}{3}, \frac{4-3}{3})$$=(1, \frac{1}{3})$给定三角形的重心为 $(1, \frac{1}{3})$。