已知:△ABC ~ △DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm 和 FD = 12 cm。求:ABC 的周长。解:根据题中给出的尺寸,现在,我们必须求出△ABC 的周长。设△ABC~△DEF,所以 AB/DE = AC/DF = BC/EF。考虑 AB/DE = AC/DE,4/6 = AC/12。交叉相乘得到,=> AC = (4 × 12) / 6 => AC = 48 / 6 => AC = 8 cm。然后,考虑 AB/DE = BC/EF,=> 4/6 = BC/9,=> BC = (4 × 9) / 6,=> BC = 36 / 6,=> BC = 6 cm。因此,△ABC 的周长 = AB + BC + AC = 4 + 6 + 8 = 18 cm。阅读更多
已知:在给定图中 DE||BC,AD = x,DB = x-2,AE = x+2,EC = x-1。求:x 的值。解:在△ABC 中,DE||BC,∴ AD/DB = AE/EC [根据基本比例定理] => x/(x-2) = (x+2)/(x-1) => x(x−1) = (x+2)(x−2) => x²−x = x²−4 => x = 4。因此,x 的值为 4。
已知:边长为 8 cm 的等边三角形。求:等边三角形的高。解:△ABC 是等边三角形。 AD⊥BC 现在在△ADB 和△ADC 中,AB=BC [等边三角形的边] ∠1=∠2=90° AD=AD [公共边] ∴△ADB≅△ADC [根据 RHS 全等准则] => BD=DC [全等三角形对应边相等] ∴ BD=DC=BC/2=8/2=4 cm ∴ 根据勾股定理,在直角三角形…阅读更多
已知:ABCD 是平行四边形,P 是 BC 边上的一点,DP 的延长线与 AB 的延长线相交于 L。求证:DP/PL = DC/BL。证明:如图所示,平行四边形 ABCD,其中 P 是 BC 边上的一点,使得 DP 的延长线与 AB 的延长线相交于 L。在△ALD 中,我们有 BP||AD ∴ LB/BA = LP/PD => BL/AB = PL/DP => BL/DC = PL/DP [AB=DC] 对两边取倒数 => DP/PL = DC/BL 证毕。阅读更多
(a) 如果镜子对放置在其前面的所有位置的物体的成像始终是缩小的、正立的和虚像,则镜子的类型是凸面镜。这种镜子用作汽车的后视镜,因为这种类型的镜子可以提供正立的、更宽的视野来观察汽车后面的物体。(b) 球面镜的曲率半径是极点 (P) 和曲率中心 (C) 之间的距离。已知:曲率半径,R = +24cm。求:球面镜的性质和焦距 (f)。解:我们知道曲率半径…阅读更多
已知:两个相似三角形的面积分别为 36 cm² 和 100 cm²。如果较大三角形的一条边的长度为 20 cm。求:较小三角形对应边的长度。解:已知,较小三角形的面积 = 36 cm²,较大三角形的面积 = 100 cm²,较小三角形一边的长度 = 3 cm。设较大三角形对应边的长度为 x cm。已知,面积(较大三角形)/面积(较小三角形) = (较大三角形边长)²/(较小三角形边长)² 100/36 = x²/3² => 36x = 100 × 3² => x² = 900/36 => x² = 25 => x = ±√25 => x = ±5 因为三角形的边长不能为负数。因此,对应边的长度为…阅读更多
已知:图中∠ACB = ∠CDA,AC = 8 cm,AD = 3 cm。求:BD。解:因为∠CDA=90° => ∠ACB=90° 在△ACD 中,cosA = AD/AC = 3/8 在△ABC 中,cosθ = AC/AB => 3/8 = 3/AB => AB = 8 cm => BD = 8 - 3 = 5 cm 因此,BD = 5 cm。
(a) 从序号 3 可以看出,透镜的曲率半径(从透镜的光学中心到曲率中心的距离)为 40 cm,因为物距 (u) 等于像距 (v),均为 40 cm。当物体放在凸透镜的曲率中心(或 2F)时,其像在距透镜相同距离处形成,但在透镜的另一侧。而且,我们知道焦距是曲率半径的一半。因此,透镜的焦距为…阅读更多
已知:梯形ABCD中,AB∥DC,P、Q分别为AD和BC上的点,且PQ∥DC。已知PD = 18 cm,BQ = 35 cm,QC = 15 cm。 求:AD的长度。 解: 作图:连接BD 在△ABD中,PO∥AB [∵ PQ ∥AB] ⇒ DP/AP = DO/OB ---- (i) [根据基本比例定理] 在△BDC中,OQ∥DC [∵ PQ ∥DC] BQ/QC = OB/OD [根据基本比例定理] ⇒ ... 阅读更多
已知:菱形的两条对角线的长度分别为16 cm和12 cm。 求:菱形的边长。 解:菱形的对角线互相垂直平分。 因为d₁=16 cm,d₂=12 cm 所以,d₁/2 = 16/2 = 8,d₂/2 = 12/2 = 6 根据勾股定理: a² = (d₁/2)² + (d₂/2)² ⇒ a² = 8² + 6² ⇒ a = √100 = 10 cm 所以,菱形的边长为10 cm。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP

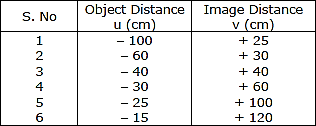 (a) 凸透镜的焦距是多少?说明理由。(b) 指出哪个观测值不正确。你得出这个结论的依据是什么?(c) 选择合适的比例尺,并为序号 2 的观测值绘制光路图。此外
(a) 凸透镜的焦距是多少?说明理由。(b) 指出哪个观测值不正确。你得出这个结论的依据是什么?(c) 选择合适的比例尺,并为序号 2 的观测值绘制光路图。此外