如果$ABCD$是平行四边形，$P$是边$BC$上的一点，且$DP$的延长线交$AB$的延长线于$L$，则证明$\frac{DP}{PL}=\frac{DC}{BL}$。

已知：$ABCD$是平行四边形，$P$是边$BC$上的一点，且$DP$的延长线交$AB$的延长线于$L$。

求证：$\frac{DP}{PL}=\frac{DC}{BL}$。

解答

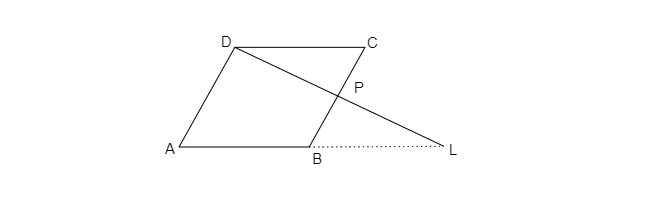
如图所示，平行四边形$ABCD$中，$P$是边$BC$上一点，$DP$延长线交$AB$延长线于$L$。

在$\vartriangle ALD$中，我们有

$BP||AD$

$\therefore \frac{LB}{BA}=\frac{LP}{PD}$

$\Rightarrow \frac{BL}{AB}=\frac{PL}{DP}$

$\Rightarrow \frac{BL}{DC}=\frac{PL}{DP}$     [$AB=DC$]

两边取倒数

$\Rightarrow \frac{DP}{PL}=\frac{DC}{BL}$

证毕。

教程点

更新于：2022年10月10日

66 次浏览

开启您的职业生涯

完成课程获得认证

开始学习