数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：给定的方程为：$4x\ -\ y\ =\ 4, \ 3x\ +\ 2y\ =\ 14$需要做的：我们需要解决给定的线性方程组，并对给定直线和 y 轴围成的区域进行阴影。解：为了用图形表示上述方程，我们需要每个方程至少两个解。对于方程 $4x-y=4$，$y=4x-4$如果 $x=1$ 则 $y=4(1)-4=4-4=0$如果 $x=2$ 则 $y=4(2)-4=8-4=4$$x$$1$$2$$y$$0$$4$对于方程 $3x+2y=14$，$2y=14-3x$$y=\frac{14-3x}{2}$如果 $x=4$ 则 $y=\frac{14-3(4)}{2}=\frac{14-12}{2}=\frac{2}{2}=1$如果 $x=2$ 则 $y=\frac{14-3(2)}{2}=\frac{14-6}{2}=\frac{8}{2}=4$$x$$4$$2$$y$$1$$4$y 轴的方程为 $x=0$。上述情况可以用图形表示如下：直线 AB 和 CD 分别表示方程 $4x-y=4$ 和 $3x+2y=14$。阴影区域是 ... 阅读更多
已知：裙子的数量比购买的裤子数量的两倍少两件。此外，裙子的数量比购买的裤子数量的四倍少四件。=需要做的：我们需要建立一元一次方程组并用图形方法求解。此外，我们还需要找到 Champa 购买的裤子和裙子的数量。解：假设 Champa 购买的裤子和裙子的数量分别为 $x$ 和 $y$。根据题意，$y = 2x-2$.....(i)$y = 4x-4$.....(ii)为了用图形表示上述方程，我们需要每个方程至少两个解。对于方程 $y=2x-2$，如果 $x=1$ 则 $y=2(1)-2=2-2=0$如果 $x=0$ ... 阅读更多
已知：5 支铅笔和 7 支钢笔共计 50 卢比，而 7 支铅笔和 5 支钢笔共计 46 卢比。需要做的：我们需要建立一元一次方程组并用图形方法求解。此外，我们还需要找到一支铅笔和一支钢笔的价格。解：假设一支铅笔和一支钢笔的价格分别为 $x$ 和 $y$。根据题意，$5x + 7y = 50$.....(i)$7x + 5y = 46$.....(ii)为了用图形表示上述方程，我们需要每个方程至少两个解。对于方程 $5x+7y=50$，$7y=50-5x$$y=\frac{50-5x}{7}$如果 $x=3$ 则 $y=\frac{50-5(3)}{7}=\frac{50-15}{7}=\frac{35}{7}=5$如果 $x=10$ 则 $y=\frac{50-5(10)}{7}=\frac{50-50}{7}=\frac{0}{7}=0$$x$$3$$10$$y$$5$$0$对于方程 $7x+5y=46$，$5y=46-7x$$y=\frac{46-7x}{5}$如果 $x=3$ ... 阅读更多
已知：给定的分数为 $\frac{18}{54}$ 和 $\frac{23}{69}$。需要做的：我们需要判断给定的分数是否相等。解：$\frac{18}{54}$ 化成最简形式为，$\frac{18}{54}=\frac{18\times1}{18\times3}$$=\frac{1}{3}$$\frac{23}{69}$ 化成最简形式为，$\frac{23}{69}=\frac{23\times1}{23\times3}$$=\frac{1}{3}$因此，$\frac{18}{54}=\frac{23}{69}=\frac{1}{3}$ 。$\frac{18}{54}$ 和 $\frac{23}{69}$ 相等。
$已知$初始速度，( u) =0$a=2.5m/s^{2}$人与公交车之间的距离=45m$从运动的第二个方程，$s=ut+\frac{1}{2} at^{2}$代入方程中的给定值，我们得到公交车行驶的距离$s=0+\frac{1}{2} 2.5t^{2}$s=\frac{2.5t^{2}}{2} \ ...........................( 1)$假设，u=人的初始速度$ \begin{array}{l} 根据题意，人需要在时间 t 内走完 ( 45+s) m 的距离才能追上公交车，可以表示为 \end{array}$$ut=45+s$$ut=45+\frac{2.5t^{2}}{2}$$ut=45+1.25t^{2}$$u=\frac{45+1.25t^{2}}{t}$$u=\frac{45}{t} +\frac{1.25t^{2}}{t}$$u=\frac{45}{t} +1.25t\ ..........................( 2)$$对于最小速度，u 的最小值为：$$\frac{du}{dt} =0$$-\frac{45}{t^{2}} +1.25=0$$-\frac{45}{t^{2}} =-1.25$$45=1.25t^{2}$$t^{2} =\frac{45}{1.25}$$t^{2} =36$$t=\sqrt{36}$$t=6sec$$从方程 ( 2) ，$$u_{min} =\frac{45}{6} +1.25\times 6$$u_{min} =7.5+7.5$$u_{min} =15m/s$$因此， ... 阅读更多
已知：给定的表达式为 $16(2p-3q)^2-4(2p-3q)$。需要做的：我们需要对给定的表达式进行因式分解。解：$16(2p-3q)^2-4(2p-3q)=4(2p-3q)[4(2p-3q)-1]$$=4(2p-3q)(8p-12q-1)$表达式 $16(2p-3q)^2-4(2p-3q)$ 的因式分解结果为 $4(2p-3q)(8p-12q-1)$。
已知：给定的表达式为 $x^2-(x-z)^2$。需要做的：我们需要对给定的表达式进行因式分解。解：$x^2-(x-z)^2=[x+(x-z)][x-(x-z)]$ (因为 $a^2-b^2=(a+b)(a-b)$)$=(2x-z)(z)$ 表达式 $x^2-(x-z)^2$ 的因式分解结果为 $(2x-z)(z)$。
已知：10 名十级学生参加了数学测验。女生人数比男生人数多 4 人。需要做的：我们需要建立一元一次方程组并用图形方法求解。此外，我们还需要找到参加测验的男生和女生的人数。解：假设班级的女生和男生人数分别为 $x$ 和 $y$。根据题意，$x + y = 10$.....(i)$x - y = 4$.....(ii)为了用图形表示上述方程，我们需要每个方程至少两个解。对于方程 $x+y=10$，$y=10-x$如果 $x=5$ 则 ... 阅读更多
(a) 仅由氢和碳组成的化合物称为烃。例如：甲烷 (CH4)、乙烷 (C2H6)、乙烯 (C2H4) 和乙炔 (C2H2) 都是烃，因为它们仅由两种元素组成：碳和氢。(b) 饱和烃是指碳原子之间以单键连接的烃，也称为烷烃。例如：甲烷和乙烷不饱和烃是指两个碳原子之间以双键或三键连接的烃。例如：乙烯和乙炔(c) 饱和环状烃：环己烷 C6H12不饱和环状烃：苯 C6H6(d) 己烷具有三个以上异构体。(e) 个数... 阅读更多
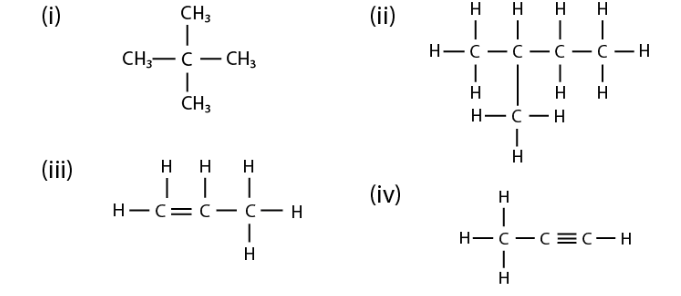
"\(a) 具有相同分子式但结构不同的有机化合物称为异构体，例如：正丁烷和异丁烷是异构体。(b) 正庚烷的异构体：2-甲基己烷。(ii) 2-甲基己烷的电子点式：(c) 该化合物的 IUPAC 名称是丁烷(d) IUPAC 名称如下：(i) 2-甲基丙烷(ii) 2-甲基丁烷(iii) 丙烯(iv) 丙炔