Tutorialspoint

更新于 2022年10月10日 10:25:57

90 次浏览

已知：数字：$\sqrt{2}$。任务：证明给定的数字是无理数。解：假设 $\sqrt{2}$ 是有理数。$\sqrt{2}=\frac{p}{q}$，其中 p 和 q 是互质整数，且 $q =0$ $\Rightarrow \sqrt{2}q=p$ $\Rightarrow 2q^{2}=p^{2}$ ...............$( i)$ $\Rightarrow 2\ 整除\ p^{2}$ $\Rightarrow 2\ 整除\ p$ ...............$( A)$ 令 $p =2c$，其中 c 为某个整数 $p^{2}= 4c^{2}$ $2q^{2}=4c^{2}$ $\Rightarrow q^{2}=2c^{2}$ $\Rightarrow 2\ 整除\ q^{2}$ $\Rightarrow 2\ 整除\ q$ ...............$( B)$ 从 $( A)$ 和 $( B)$，我们… 阅读更多

Tutorialspoint

更新于 2022年10月10日 10:25:57

3.3万+ 次浏览

已知：多项式 $x^{2}-(k+6)x+2(2k-1)$ 的零点之和等于其零点之积的一半。求：求 k 的值。解：已知多项式 $x^{2}-(k+6)x+2(2k-1)$ 是一个二次多项式。将其与 $ax^{2}+bx+c$ 比较，我们有 $a=1, b=-(k+6)$ 和 $c=2(2k-1)$ 令 $\alpha$ 和 $\beta$ 是给定多项式的零点。已知，零点之和，$\alpha+\beta=-b$ $\Rightarrow \alpha+\beta=-(-(k+6))=k+6$ 零点之积的一半，$\frac{\alpha.\beta}{2}=\frac{1}{2}×\frac{c}{a}=\frac{2(2k-1)}{2}=2k-1$ 已知：$\alpha+\beta=\frac{\alpha.\beta}{2}$ $k+6=2k-1$ $\Rightarrow 2k-k=6+1$ $\Rightarrow k=7$ 因此，k 的值为 7。 阅读更多

Tutorialspoint

更新于 2022年10月10日 10:25:57

124 次浏览

已知：父亲的年龄是两个孩子年龄之和的三倍。五年后，他的年龄将是他们年龄之和的两倍。求：求父亲现在的年龄。解：设两个儿子现在的年龄之和 = x 年 $\therefore$ 父亲的年龄 = 3x ...............$( 1)$ 五年后，儿子们的年龄之和 = (x+10) 年 父亲的年龄 = 3x+5 根据题意， 3x+5=2(x+10) $\Rightarrow 3x+5=2x+20$ $\Rightarrow 3x-2x=20-5$ $\Rightarrow x=15$ 年 因此父亲的年龄为 3x=3×15=45 年。

Tutorialspoint

更新于 2022年10月10日 10:25:57

60 次浏览

已知：一个分数，当从分子中减去 2 时变为 $\frac{1}{3}$，当从分母中减去 1 时变为 $\frac{1}{2}$ 求：求这个分数。解：设分数为 $\frac{x}{y}$。从分子中减去 2， $\frac{x-2}{y}=\frac{1}{3}$ $\Rightarrow3x-6=y$ $\Rightarrow3x-y=6 $ ...............$( 1)$ 从分母中减去 1， $\frac{x}{y-1}=\frac{1}{2}$ $\Rightarrow2x=y-1$ $\Rightarrow2x-y=-1 $ ...............$( 2)$ 从 $( 1)$ 中减去 $( 2)$， $3x-y-2x+y=6+1$ $\Rightarrow x=7$ 将 $x=7$ 代入 $( 1)$ $3(7)-y=6$ $\Rightarrow y=21-6$ $\Rightarrow y=15$ 因此，分数 = $\frac{x}{y}=\frac{7}{15}$。

Tutorialspoint

更新于 2022年10月10日 10:25:57

62 次浏览

已知：y 轴上有一个点与点 $( 5, \ - 2)$ 和 $( -3, \ 2)$ 等距。求：求这个点。解：由于该点在 y 轴上，因此 x 坐标为零。设该点为 $P( 0, \ y)$ 它到 $A( 5, \ -2)$ 和 $B( - 3, \ 2)$ 的距离相等。我们知道，如果存在两个点 $( x_{1}, y_{1})$ 和 $( x_{2}, y_{2})$，则两点之间的距离 =$\sqrt{( x_{2}-x_{1})^{2}+( y_{2}-y_{1})^{2}}$ $PA=\sqrt{( 5-0)^{2}+( -2-y)^{2}}$ $\Rightarrow PA=\sqrt{(5)^{2}+(-(2+y))^{2}}$ $\Rightarrow PA=\sqrt{25+(y+2)^{2}}$ $\Rightarrow PA=\sqrt{25+y^{2}+4+4y}$ $\Rightarrow PA=\sqrt{y^{2}+4y+29}$ $\Rightarrow ( PA)^{2}=y^{2}+4y+29$ ...............$( 1)$ 同样地， $PB=\sqrt{( -3-0)^{2}+( 2-y)^{2}}$ $\Rightarrow PB=\sqrt{( -3)^{2}+4+y^{2}-4y}$ $\Rightarrow ( PB)^{2}=9+4+y^{2}-4y$ $\Rightarrow ... 阅读更多

Tutorialspoint

更新于 2022年10月10日 10:25:57

68 次浏览

已知：连接点 $A( 2, \ 1)$ 和 $B( 5, \ -8)$ 的线段被点 $P$ 和 $Q$ 三等分，使得 $P$ 离 $A$ 更近，且 $P$ 也在线 $2x - y = 0$ 上。求：求 k 的值。解：由于线段 AB 被点 P 和 Q 三等分。当 AP:PB = 1:2 时，使用截距公式，我们有 $P( x, \ y)=( \frac{nx_{1}+mx_{2}}{m+n}, \frac{ny_{1}+my_{2}}{m+n})$ 则，P 的坐标为： $P=( \frac{1×5+2×2}{1+2}, \frac{1×(-8)+1×2}{1+2})$ $\Rightarrow P=( \frac{5+4}{3}, \frac{-8+2}{3})$ $\Rightarrow P=( \frac{9}{3}, \frac{-6}{3})$ $\Rightarrow P=( 3, -2)$ 已知点 $P( 3, \ -2)$ 在线… 阅读更多

Tutorialspoint

更新于 2022年10月10日 10:25:57

63 次浏览

已知：$( sin \theta+ cosec \theta)^{2}+( cos \theta+sec \theta)^{2} =7+ tan^{2} \theta+ cot^{2} \theta$。求：证明左边 = 右边。解：左边=$(sin \theta+ cosec \theta)^{2}+(cos \theta+sec \theta)^{2}$$=sin^{2} \theta+cosec^{2} \theta+2sin \theta cosec \theta+cos^{2} \theta+sec^{2} \theta+2cos \theta sec \theta$$=sin^{2} \theta+cos^{2} \theta+2sin \theta cosec \theta+sec^{2} \theta+cosec^{2} \theta+2cos \theta sec \theta$$=1+2+2+sec^{2} \theta+cosec^{2} \theta$ [$\because sin^{2}\theta + cos^{2}\theta=1$，$sin \theta=\frac{1}{cosec \theta}$ 和 $cos \theta=\frac{1}{sec \theta}$] $=5+1+tan^{2} \theta+1+cot^{2} \theta$ [$sec^{2} \theta=1+tan^{2} \theta$ 和 $cosec^{2} \theta=1+cot^{2} \theta$] $=7+tan^{2} \theta+cot^{2} \theta$ $=右边$ 因此证明左边 = 右边。 阅读更多

Tutorialspoint

更新于 2022年10月10日 10:25:57

69 次浏览

已知：$( 1+cot A-cosecA)( 1+ tan A+secA)=2$ 求：证明左边 = 右边。解：左边=$( 1+cot A-cosecA)( 1+ tan A+secA)$ $=( 1+\frac{cosA}{sinA}-\frac{1}{sinA})( 1+\frac{sinA}{cosA}+\frac{1}{cosA})$ $=(\frac{sinA+cosA-1}{sinA})(\frac{cosA+sinA+1}{cosA})$ $=(\frac{( sinA+cosA-1)( sinA+cosA+1)}{sinAcosA})$ $=\frac{( sinA+cosA)^{2}-( 1)^{2}}{sinAcosA}$ $=\frac{sin^{2}A+cos^{2}A+2sinAcosA-1}{sinAcosA}$ $=\frac{1+2sinAcosA-1}{sinAcosA}$ $=\frac{2sinAcosA}{sinAcosA}$ $=2$ $=右边$ 因此证明 $( 1+cot A-cosecA)( 1+ tan A+secA)=2$。

Tutorialspoint

更新于 2022年10月10日 10:25:57

112 次浏览

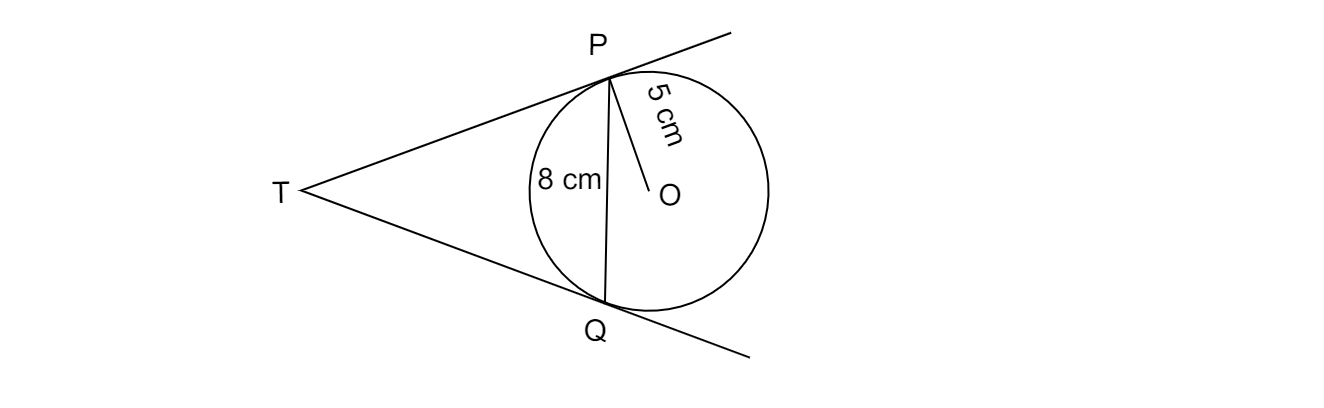
已知：弦 PQ 的长度 = 8 厘米，圆的半径 OP = 5 厘米。求：求 TP 的长度。解：已知半径 OP=OQ=5 厘米 弦长 PQ=8 厘米 OT 垂直于 PQ。因为从圆心到弦的垂线平分弦。$\therefore PM=MQ=4\ cm$ 在直角三角形 OPM 中，$(OP)^{2}=(PM)^{2} +(OM)^{2}$ $\Rightarrow(5)^{2}=(4)^{2}+(OM)^{2}$ $\Rightarrow ( OM)^{2}=25-16=9$ $\Rightarrow OM=\sqrt{9}$ $\Rightarrow OM=3\ cm$ $\angle OPT=90^{o}$ [半径垂直于接触点的切线] 在直角三角形 OPT 中，$( OT)^{2}=( PT)^{2}+( OP)^{2}$ ... 阅读更多

Tutorialspoint

更新于 2022年10月10日 10:25:55

74 次浏览

制造电极时利用了石墨的导电性。