已知:从圆外一点 R 引出两条切线 RQ 和 RP 到圆心为 O 的圆上,如果∠PRQ = 120°。要求:证明 OR = PR + RQ。解答:连接 OR。已知连接圆心和外一点的直线是切线之间夹角的角平分线。这里给定∠PRQ = 120°∠PRO=∠QRO=120°/2 = 60°我们也知道从外一点引出的切线长度相等。因此,PR=RQ。连接 OP 和 OQ。由于 OP 和 OQ 是从圆心 O 引出的半径,OP⊥PR 和 OQ⊥RQ。因此,△OPR 和 △OQR 是 ... 阅读更多
已知:两个不同的骰子一起掷出。要求:求两个骰子顶面上的数字的乘积为 6 的概率。解答:两个骰子掷出S=[(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4), (5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)]当两个骰子一起掷出时,可能的总结果数=6×6乘积为 6 的事件=( 1, 6)、( 2, 3)、( 3, 2)、( 6, 1)有利结果数=6乘积为 6 的概率=可能的结果数/可能的总结果数=6/36=1/6因此,当掷出两个骰子时,结果乘积为 6 的概率为 1/6。
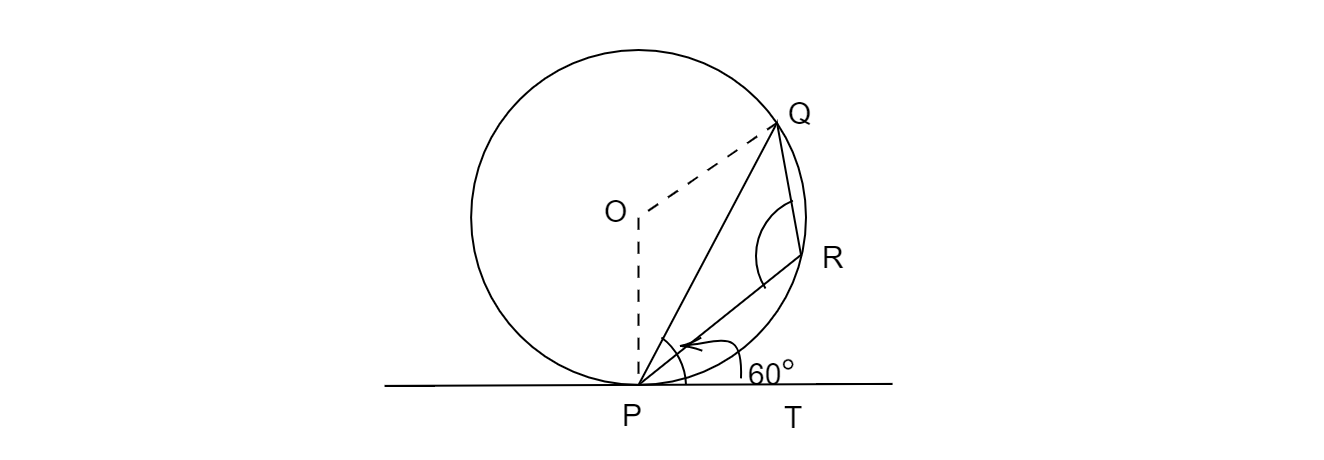
已知:圆 O 的弦 PQ 和切线 PT。其中 P 是切点。∠QPT=60°要求:求∠PRQ=?解答:∠OPT=90° (∵半径总是垂直于切点处的切线)所以,∠OPQ=∠OPT-∠QPT=90°-60°=30°现在在△OPQ 中,∠OPQ=∠OQP=30° (∵OP=OQ=圆的半径)∴ ∠POQ=180°-( 30° + 30° )=120°我们知道△OPQ 有一个反射△PEQ。∴ ∠POQ=∠PRQ=120°因此∠PRQ=120°。 阅读更多
已知:二次方程 px²-2√5 px+15=0 有两个相等的根。要求:求 P 的值。解答:二次方程 px²-2√5 px+15=0,将其与标准二次方程 ax²+bx+c=0 进行比较我们有 a=p, b=2√5p,c=15对于相等根,其判别式 D=0 或 b²-4ac=0( 2√5 p)²-4×p×15=020p² -60p=020p( p-3)=0p( p-3)=0⇒ p=0、3但是,p = 0 不可能。因此,当 p=0、3 时,给定方程有两个相等的根。
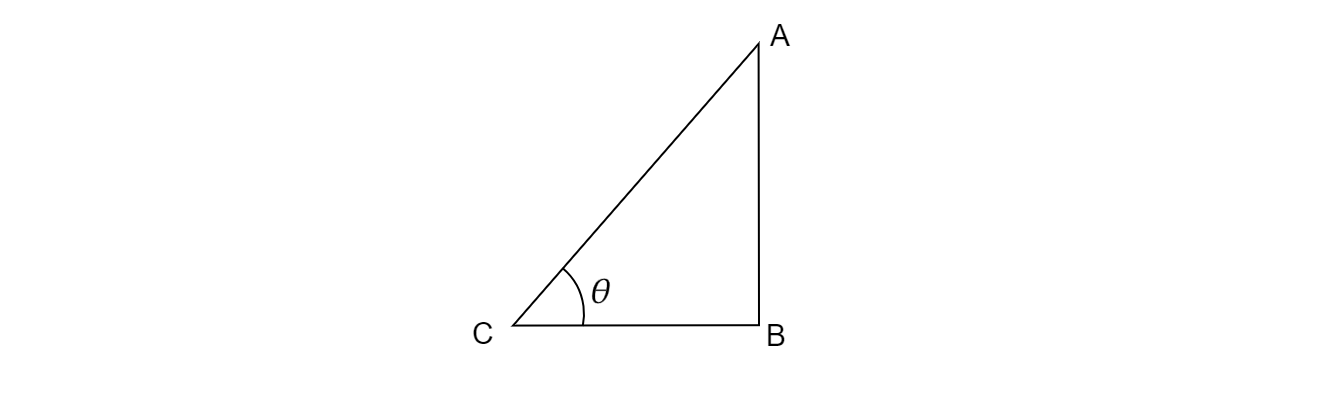
已知:塔的高度 AB=20 米,其在地面上的影子 BC=20√3 米。要求:求太阳的高度角。解答:设 AB 为塔,BC 为其影子,θ 为太阳的高度角。AB = 20、BC = 20、θ=?在△ABC 中,tanθ=AB/BC (∵tanθ =垂直边/底边)⇒ tanθ =20/20√3⇒ tanθ =1/√3但是已知 tan30°=1/√3⇒ tanθ =tan30°⇒ θ =30°太阳的高度角为 30°。
已知:R = 20 欧姆I = 2 安培求:电位差 V解答:根据欧姆定律:V=I × RV=2 × 20V=40 伏特
已知:V = 3 伏特I = 5 安培求:电阻 R解答:根据欧姆定律:R=V/I R=3/5 R = 0.6 欧姆
欧姆定律指出电位差与电流之间的关系。
良导体:电阻非常低的物质称为良导体。例如,铜和铝。电阻器:与导体相比,电阻相对较高的物质称为电阻器。例如,镍铬合金和锰铜合金。绝缘体:电阻无限大的物质称为绝缘体。例如,橡胶、木材、塑料。
良导体:汞、铝、铁、金属硬币电阻器:锰铜合金、镍铬合金绝缘体:橡胶、聚乙烯、木材、酚醛塑料、纸、泡沫塑料

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP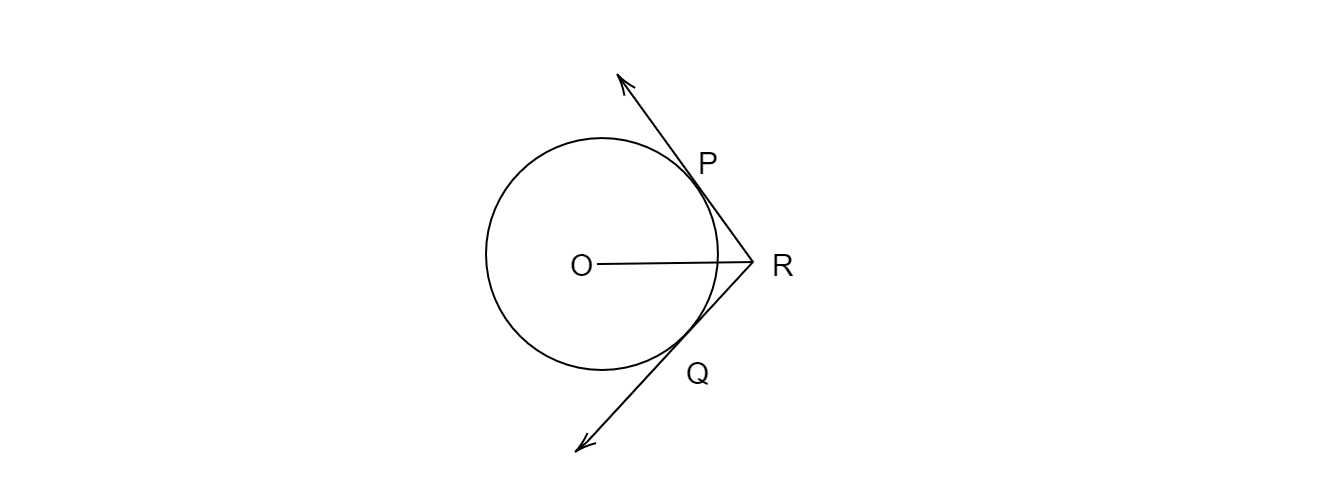 "\
"\
 "\
"\ "\
"\