数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
质量的 SI 单位是千克 (kg)
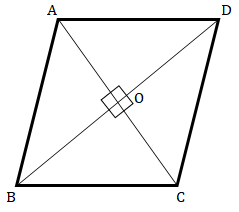
已知：四边形的对角线相等且互相垂直平分。要求：我们必须证明它是正方形。解答： 设 $ABCD$ 是一个四边形，其中对角线相等且互相垂直平分。所以，$AC=BD$ $OA=OC, OB=OD$ $\angle AOB = \angle BOC =\angle COD =\angle AOD = 90^o$要证明它是正方形，我们需要证明该四边形是平行四边形，并且其中一个角是 $90^o$。在 $\triangle AOB$ 和 $\triangle BOC$ 中，$OA=OC$ (已知)$OB=OB$ ... 阅读更多
已知：给定项为 $(+8)+(+6)+(-5)$。要求：我们必须化简给定项。解答：$(+8)+(+6)+(-5)$$(+8)+(+6)+(-5)= 8+6-5$ $[+ \times - =-]$$ = 14-5 = 9$。$(+8)+(+6)+(-5)$ 的值为 9。
"\已知：菱形的对角线长为 $24\ cm$ 和 $10\ cm$。要求：这里，我们必须找到菱形的每条边。解答：我们知道，菱形的对角线互相垂直平分。因此，$AO = OC = \frac{24}{2}\ cm = 12\ cm$ 且 $BO = OD = \frac{10}{2}\ cm = 5\ cm$在 $∆AOB$ 中，根据勾股定理，$AB^2 = AO^2 + BO^2$$AB^2= 12^2 + 5^2$$AB^2= 144 + 25$$AB^2= 169$$AB = \sqrt{169} = 13\ cm$菱形的各边都相等。因此，$AB = BC = CD = AD = 13\ cm$。菱形的每条边长为 $13\ cm$。
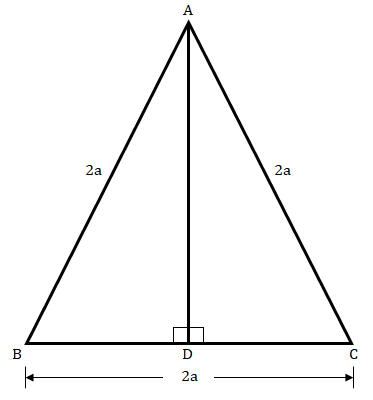
"\已知：在 $∆ABC$ 中，$AB\ =\ BC\ =\ CA\ =\ 2a$ 且 $AD\ ⊥\ BC$。要求：我们必须证明：(i) $AD\ =\ a\sqrt{3}$ (ii) 面积 $(∆ABC)\ =\ \sqrt{3}a^2$解答：(i) 在 $∆ABD$ 和 $∆ACD$ 中，$\angle ADB = \angle ADC = 90^o$$AB = AC$ (已知)$AD = AD$ (公共边)因此，$∆ABD ≅ ∆ACD$ (根据 RHS 全等)这意味着，$BD = CD = a$ (全等三角形的对应边相等)在 $∆ABD$ 中，根据勾股定理，$AD^2 + BD^2 = AB^2$$AD^2 + a^2 = (2a)^2$$AD^2 = 4a^2 – a^2 = 3a^2$$AD = \sqrt{3a^2}$$AD = \sqrt{3}a$(ii) 面积 $(∆ABC) = \frac{1}{2} \times BC \times AD$ ... 阅读更多
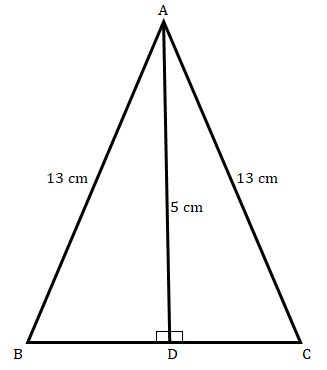
"\已知：在给定的等腰三角形 $ABC$ 中，$AB\ =\ AC\ =\ 13\ cm$，且从 $A$ 到 $BC$ 的高为 $5\ cm$。要求：我们必须找到 $BC$。解答：在 $∆ADB$ 中，使用勾股定理，$AD^2 + BD^2 = AB^2$$5^2 + BD^2 = 13^2$$BD^2 = 169 – 25$ $BD^2= 144$$BD = \sqrt{144} = 12\ cm$类似地，在 $∆ADC$ 中，应用勾股定理，$AC^2 = AD^2 + DC^2$$13^2 = 5^2 + DC^2$$DC^2 = 169-25$$DC = \sqrt{144} = 12\ cm$因此，$BC = BD + DC = (12+12)\ cm = 24\ cm$ $BC$ 的长度为 $24\ cm$。
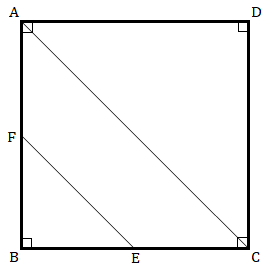
"\已知：$ABCD$ 是一个正方形。$F$ 是 $AB$ 的中点。$BE$ 是 $BC$ 的三分之一。$∆\ FBE\ =\ 108\ cm^2$，要求：我们必须找到 $AC$ 的长度。解答：设正方形的边长为 $x$。这意味着，$AB = BC = CD = DA = x\ cm$$AF = FB = \frac{x}{2}\ cm$ ($F$ 是 $AB$ 的中点)$BE = \frac{x}{3}\ cm$ ($BE$ 是 $BC$ 的三分之一)$∆FBE$ 的面积 $= \frac{1}{2} \times BE \times FB$$108 = \frac{1}{2} \times (\frac{x}{3}) \times (\frac{x}{2})$$\frac{x^2}{12} = 108$$x^2= 108\times12$$x^2=1296$$x = \sqrt{1296}$$x = 36\ cm$在 $∆ABC$ 中，根据勾股定理，$AC^2 = AB^2 + ... 阅读更多
该反应的平衡化学方程式如下所示：锌 + 硝酸银 -------> 硝酸锌 + 银 $Zn\ +\ 2AgNO_{3} \ \rightarrow \ Zn( NO_{3})_{2} \ +\ 2Ag$
酸败是用来表示由于空气氧化（当脂肪和油类食品暴露在空气中相当长的时间时），导致脂肪和油类食品产生难闻的气味和味道的术语。
抗氧化剂是添加到含有脂肪和油的食品中以防止酸败发生的化学物质的通用名称。