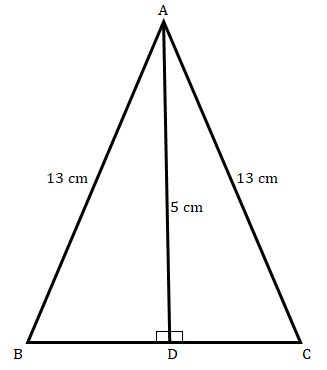
在一个等腰三角形 $ABC$ 中，如果 $AB\ =\ AC\ =\ 13\ cm$，且从 $A$ 到 $BC$ 的高为 $5\ cm$，求 $BC$ 的长度。
"\n

已知

在给定的等腰三角形 $ABC$ 中，$AB\ =\ AC\ =\ 13\ cm$，且从 $A$ 到 $BC$ 的高为 $5\ cm$。

要求

我们要求 $BC$ 的长度。

解

在 $∆ADB$ 中，

根据勾股定理，

$AD^2 + BD^2 = AB^2$

$5^2 + BD^2 = 13^2$

$BD^2 = 169 – 25$

$BD^2= 144$

$BD = \sqrt{144} = 12\ cm$

类似地，

在 $∆ADC$ 中，

应用勾股定理，

$AC^2 = AD^2 + DC^2$

$13^2 = 5^2 + DC^2$

$DC^2 = 169-25$

$DC = \sqrt{144} = 12\ cm$

因此，

$BC = BD + DC = (12+12)\ cm = 24\ cm$

$BC$ 的长度为 $24\ cm$。

教程点

更新于: 2022年10月10日

58 次浏览

开启您的 职业生涯

通过完成课程获得认证

开始学习