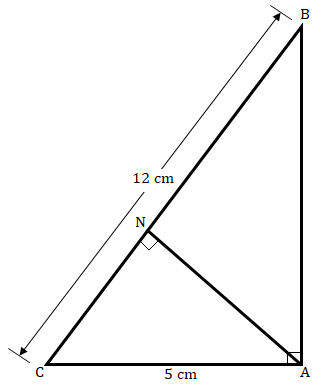
在三角形$ABC$中，$∠\ A\ =\ 90^o$，$AN\ ⊥\ BC$，$BC\ =\ 12\ cm$，$AC\ =\ 5\ cm$。求$ΔANC$和$ΔABC$面积的比值。
"\n

已知

在三角形$ABC$中，$∠\ A\ =\ 90^o$，$AN\ ⊥\ BC$，$BC\ =\ 12\ cm$，$AC\ =\ 5\ cm$。

求解

我们需要求$ΔANC$和$ΔABC$面积的比值。

解答

在$ΔANC$和$ΔABC$中，

$\angle ACN = \angle ACB$（公共角）

$\angle ANC = \angle BAC=90^o$

因此，

$ΔANC ∼ ΔABC$（根据角角相似）

我们知道，

两个相似三角形的面积之比等于它们对应边平方之比。

这意味着，

$\frac{ar(ΔANC)}{ar(ΔABC)} = (\frac{AC}{BC})^2$

                                                 $= (\frac{5}{12})^2 = \frac{25}{144}$

因此，$ar(ΔANC):ar(ΔABC) = 25:144$。

Tutorialspoint

更新于: 2022年10月10日

35 次浏览

开启您的 职业生涯

通过完成课程获得认证

开始学习