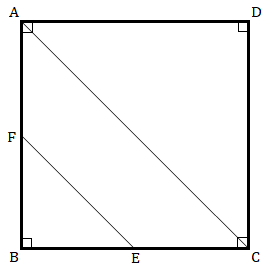
$ABCD$ is a square. $F$ is the mid-point of $AB$. $BE$ is one third of $BC$. If the area of $∆\ FBE\ =\ 108\ cm^2$, find the length of $AC$.

已知

$ABCD$是一个正方形。

$F$是$AB$的中点。

$BE$是$BC$的三分之一。

$\triangle FBE$的面积$= 108 cm^2$
 求解

我们需要求出$AC$的长度。

解题过程

设正方形边长为$x$。

这意味着：

$AB = BC = CD = DA = x\ cm$

$AF = FB = \frac{x}{2}\ cm$ ($F$是$AB$的中点)

$BE = \frac{x}{3}\ cm$ ($BE$是$BC$的三分之一)

$\triangle FBE$的面积 $= \frac{1}{2} \times BE \times FB$

$108 = \frac{1}{2} \times (\frac{x}{3}) \times (\frac{x}{2})$

$\frac{x^2}{12} = 108$

$x^2= 108\times12$

$x^2=1296$

$x = \sqrt{1296}$

$x = 36\ cm$

在$\triangle ABC$中，

根据勾股定理，

$AC^2 = AB^2 + BC^2$

$AC^2 = x^2 + x^2$

$AC^2=2x^2$

$AC^2 = 2(36)^2$

$AC = \sqrt{2(36)^2}$

$AC= 36 \times \sqrt{2}$

$AC = 36\times1.414 = 50.904\ cm$

因此，$AC$的长度是$50.904\ cm$。

Tutorialspoint

更新于：2022年10月10日

浏览量：20

开启你的职业生涯

完成课程获得认证

开始学习