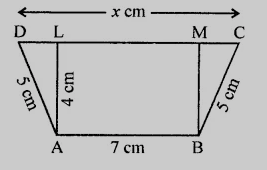
如图所示，$ABCD$是一个梯形，其中$AB = 7\ cm, AD = BC = 5\ cm, DC = x\ cm$，$AB$和$DC$之间的距离为$4\ cm$。求$x$的值和梯形$ABCD$的面积。
"\n

已知

$ABCD$是一个梯形，其中$AB = 7\ cm, AD = BC = 5\ cm, DC = x\ cm$，$AB$和$DC$之间的距离为$4\ cm$。

要求

我们需要求出$x$的值和梯形$ABCD$的面积。

解答

在$\triangle \mathrm{ADL}$中，

$\mathrm{AD}^{2}=\mathrm{AL}^{2}+\mathrm{LD}^{2}$

$5^{2}=4^{2}+\mathrm{LD}^{2}$

$25=16+\mathrm{LD}^{2}$

$\mathrm{LD}^{2}=25-16$

$=9$

$=(3)^{2}$

$\Rightarrow \mathrm{LD}=3 \mathrm{~cm}$

类似地，

$\mathrm{AL}$和$\mathrm{BM}$是垂直于$\mathrm{CD}$的垂线$\mathrm{MC}=\mathrm{LD}=3 \mathrm{~cm}$

$\mathrm{LM}=\mathrm{AB}=7 \mathrm{~cm}$

因此，

$x=\mathrm{DL}+\mathrm{LM}+\mathrm{MC}$

$=3+7+3$

$=13 \mathrm{~cm}$

梯形$ABCD$的面积$=\frac{1}{2}(a+b) \times h$

$=\frac{1}{2}(7+13) \times 4$

$=\frac{1}{2} \times 20 \times 4$

$=40 \mathrm{~cm}^{2}$

教程点

更新于: 2022年10月10日

61 次浏览

开启你的职业生涯

通过完成课程获得认证

立即开始