如图所示，$ABCD$ 是一个平行四边形，$AE \perp DC$ 且 $CF \perp AD$。

---

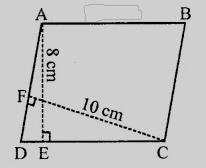
已知

$ABCD$ 是一个平行四边形，$AE \perp DC$ 且 $CF \perp AD$。

$AD = 6\ cm，CF = 10\ cm，AE = 8\ cm$。

要求

求 $AB$ 的长度。

解答

我们知道：

平行四边形的面积 = 底 × 高

因此：

平行四边形 $ABCD$ 的面积 = $AB \times AE$

$= AB \times 8$

$= 8AB\ cm^2$

这意味着：

高 $CF = 10\ cm$

面积 = 底 (AD) × 高 (CF)

$= 6 \times 10$

$=60\ cm^2$

因此：

$8AB=60$

$AB=\frac{60}{8}$

$AB=7.5\ cm$

因此，$AB = 7.5\ cm$。