数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
已知：铁路线上有 11 个车站。要求：我们必须找到为了满足从任意一个车站到其他任意一个车站的所有可能的预订，必须打印多少种不同的单程票。解答： 铁路线上有 11 个车站。从第一个车站，可以预订 10 张不同的票到 10 个不同的车站。类似地，从每个车站，都可以预订 10 张不同的票到 10 个不同的车站。所以，$11 \times 10 = 110$因此，总共必须打印 110 种不同的单程票。
半圆的面积：圆的面积 $= πr^2$其中，r - 半径；π - 常数 半圆的面积是圆面积的一半。因此，半圆的面积 $= \frac{1}{2} πr^2$。
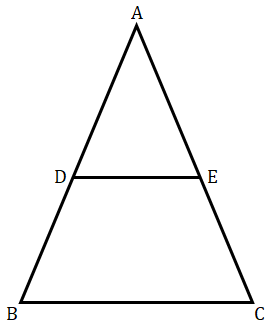
"\已知：在 $Δ\ ABC$ 中，$D$ 和 $E$ 分别是边 $AB$ 和 $AC$ 上的点，使得 $DE\ ||\ BC$。$AD\ =\ 4x\ –\ 3$，$AE\ =\ 8x\ –\ 7$，$BD\ =\ 3x\ –\ 1$，以及 $CE\ =\ 5x\ –\ 3$。要求：我们必须找到 $x$ 的值。解答：$DE\ ||\ BC$（已知）因此，根据基本比例定理，$\frac{AD}{DB}\ =\ \frac{AE}{EC}$$\frac{4x-3}{3x-1} =\frac{8x-7}{5x-3}$$(5x-3)( 4x-3) =( 8x-7)( 3x-1)$$5x( 4x-3) -3( 4x-3) =8x( 3x-1) -7( 3x-1)$$20x^{2} -15x-12x+9=24x^{2} -8x-21x+7$$( 24-20) x^{2} +( -8-21+12+15) x+7-9=0$$4x^{2} -2x-2=0$$2x^{2} -x-1=0$$2x^{2} -2x+x-1=0$$2x( x-1) +1( x-1) =0$$( x-1)( 2x+1) =0$$x-1=0$ 或 $2x+1=0$$x=1$ 或 $2x=-1$$x=1$ 或 $x=\frac{-1}{2}$三角形的边不能为 ... 阅读更多
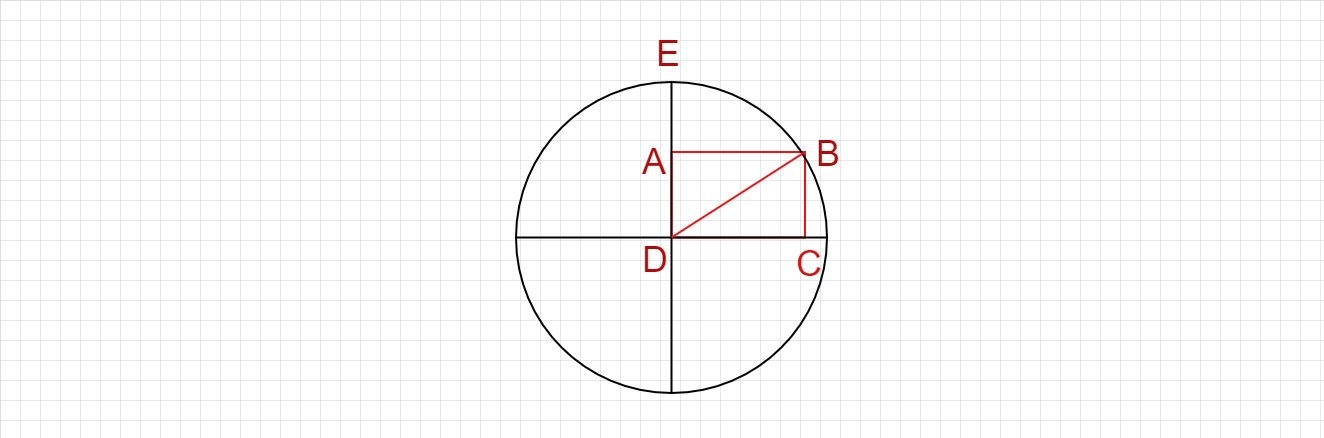
"\已知：在给定图形中，$AE =8 cm$ 且 $AD=5 cm$。要求：我们必须找到矩形的周长。解答：在以下图形中， $AE+AD = DE$ $5+8 = 13 cm$$DE = 13 cm$DE 和 DB 是圆的半径。所以，$DE = DB = 13 cm$。 $BD$ 是矩形 $ABCD$ 的对角线，也是三角形 $ABD$ 的斜边。因此，在 $\triangle ABD$ 中， $AB^2 + AD^2 = BD^2$$AB^2 + 5^2 + 13^2$$AB^2 + 25 = 169$$AB^2 = 169-25$$AB^2 = 144$$AB=12 cm$。所以，矩形的长度是 ... 阅读更多
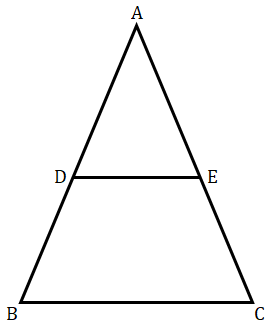
已知：在 $Δ\ ABC$ 中，$D$ 和 $E$ 分别是边 $AB$ 和 $AC$ 上的点，使得 $DE\ ||\ BC$。$AD =8x-7 cm$，$AE =5x-3 cm$，$DB =4x-3 cm$ 以及 $EC =3x-1 cm$。要求：我们必须找到 $x$ 的值。解答：$DE\ ||\ BC$（已知）因此，根据基本比例定理，$\frac{AD}{DB}\ =\ \frac{AE}{EC}$$ \begin{array}{l}\frac{8x-7}{5x-3} =\frac{4x-3}{3x-1}\\\\( 8x-7)( 3x-1) =( 4x-3)( 5x-3)\\\\8x( 3x-1) -7( 3x-1) =4x( 5x-3) -3( 5x-3)\\\\24x^{2} -8x-21x+7=20x^{2} -12x-15x+9\\\\( 24-20) x^{2} +( -8-21+12+15) x+7-9=0\\\\4x^{2} -2x-2=0\\\\2x^{2} -x-1=0\\\\2x^{2} -2x+x-1=0\\\\2x( x-1) +1( x-1) =0\\\\( x-1)( 2x+1) =0\\\\x-1=0\ 或\ 2x+1=0\\\\x=1\ 或\ 2x=-1\\\\x=1\ 或\ x=\frac{-1}{2}\end{array}$三角形的边不能为负数。因此，$x$ 的值 ... 阅读更多
当速度不恒定时，可能有两种情况。匀速运动：匀速运动是指物体在相等时间间隔内运动相等距离的运动。直线匀速运动的距离-时间图的性质如下所示。 非匀速运动：但非匀速运动是指物体在相等时间间隔内运动不相等距离的运动。它是一条弯曲的路径，如下所示。
"\已知：在给定图形中，如果 $PR=12 cm, QR = 6 cm$ 且 $PL=8cm$。要求：我们必须找到 $QM$ 的长度。解答：$\triangle PLR$ 是一个直角三角形。根据毕达哥拉斯定理，$PL^2+LR^2=PR^2$$8^2+LR^2=12^2$$64+LR^2=144$$LR^2=144-64=80$$LR=\sqrt{80}$$LR=4\sqrt{5}$$LR = LQ+QR$$LQ=LR-QR$$LQ=4\sqrt{5}-6$我们知道三角形的面积是 $\frac{1}{2} \times b \times h$所以，$\triangle PLR$ 的面积 $= \frac{1}{2} \times LR \times PL$ $ = \frac{1}{2} \times 4\sqrt{5} \times 8$ ... 阅读更多
(a) 平衡化学方程式在反应的左侧和右侧具有相同数量的每种元素的原子。它在反应物和产物中具有各种元素的相等质量。例如： $Ca( OH)_{2} \ ( aq) \ +CO_{2\ }( g) \ \rightarrow \ CaCO_{3} \ ( s) \ +\ H_{2} O\ ( l)$ '+' 读作“与…反应”，箭头“→”表示“生成”。左侧的化学式表示起始物质，称为反应物。化学方程式应该平衡以满足化学反应的质量守恒定律。（该定律指出 ... 阅读更多
"\已知：在 $Δ\ ABC$ 中，$D$ 和 $E$ 分别是边 $AB$ 和 $AC$ 上的点，使得 $DE\ ||\ BC$。$AD\ =\ x\ cm$，$AE = x -2 cm$，$DB\ =\ x\ +\ 2\ cm$ 以及 $EC\ =\ x\ –\ 1$。要求：我们必须找到 $x$ 的值。解答：$DE\ ||\ BC$（已知）因此，根据基本比例定理，$\frac{AD}{DB}\ =\ \frac{AE}{EC}$$ \begin{array}{l}\frac{x}{x-2} =\frac{x+2}{x-1}\\\\x( x-1) =( x-2)( x+2)\\\\x^{2} -x=x^{2} -4\\\\x=4\ cm\end{array}$$x$ 的值为 $4 cm$。
(a) 用化学符号和相关物质的化学式来表示化学反应的方法称为化学方程式。例如：锌金属与稀硫酸反应生成硫酸锌和氢气。该方程式写成：$Zn\ ( s) \ +\ H_{2} SO_{4} \ ( aq) \ \rightarrow \ ZnSO_{4} \ ( aq) \ +\ H_{2} \ ( g) +热量$(b) 平衡的化学方程式中，反应物和生成物中各种元素的原子数必须相等。反应物和生成物中各种元素的质量也必须相等。它遵循质量守恒定律... 阅读更多