数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装学
法学
当氢气通过氧化铜时，会生成铜和水蒸气。该反应的平衡方程式为：$H_{2} +CuO\ \rightarrow \ Cu\ +H_{2} O$(i) 元素：氢气 (H2) 和铜 (Cu)(ii) 化合物：氧化铜 (CuO) 和水 (H2O)(iii) 反应物：氢气 (H2) 和氧化铜 (CuO)(iv) 产物：铜 (Cu) 和水 (H2O)(v) 金属：铜 (Cu)(vi) 非金属：氢气 (H2)
(a) 使化学方程式更具信息量的几种方法包括：(i) 指明反应物和产物的物理状态。例如：气态用符号 (g) 表示，水溶液用 (aq) 表示。$Zn\ ( s) \ +\ H_{2} SO_{4} \ ( aq) \ \rightarrow \ ZnSO_{4} \ ( aq) \ +\ H_{2} \ ( g) +Heat$ (ii) 指明反应中发生的热量变化。例如，放热反应在产物侧写 "+ Heat" 或 "+ Heat energy" 或 "+ Energy" ... 阅读更多
"\已知：在 $Δ\ ABC$ 中，$D$ 和 $E$ 分别是边 $AB$ 和 $AC$ 上的点，使得 $DE\ ||\ BC$。$\frac{AD}{BD}\ =\ \frac{4}{5}$ 且 $EC\ =\ 2.5\ cm$。求解：我们需要求 $AE$ 的长度。解：$DE\ ||\ BC$（已知）根据基本比例定理，$\frac{AD}{BD}\ =\ \frac{AE}{CE}$$\frac{4}{5}=\frac{AE}{2.5}$$AE=\frac{4\times2.5}{5}$$AE=\frac{10}{5}$$AE=2 cm$$AE$ 的长度为 $2 cm$。
(a) 下面给出一个化学反应的例子：镁条在空气中加热生成一种叫做氧化镁的白色粉末。$2Mg\ ( s) \ +\ O_{2}( g) \ \rightarrow \ 2MgO\ ( s)$(b) 当稀硫酸倒在锌粒上时，温度会升高，会产生氢气$Zn\ ( s) \ +\ H_{2} SO_{4} \ ( aq) \ \rightarrow \ ZnSO_{4} \ ( aq) \ +\ H_{2} \ ( g) +Heat$(c) 向硝酸铅溶液中加入碘化钾溶液时发生的化学反应的两个特征是... 阅读更多
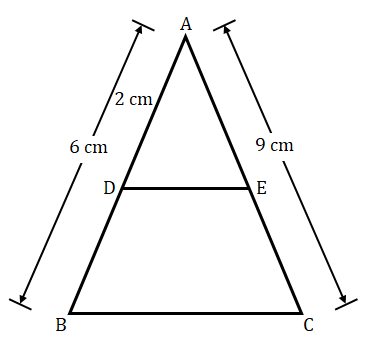
"\已知：在 $Δ\ ABC$ 中，$D$ 和 $E$ 分别是边 $AB$ 和 $AC$ 上的点，使得 $DE\ ||\ BC$。$AD\ =\ 2\ cm$，$AB\ =\ 6\ cm$ 且 $AC\ =\ 9\ cm$。求解：我们需要求 $AE$ 的长度。解：$DE\ ||\ BC$（已知）根据基本比例定理，$\frac{AD}{DB}\ =\ \frac{AE}{EC}$这意味着，$\frac{DB}{AD}\ =\ \frac{EC}{AE}$两边都加 1，$\frac{DB}{AD} + 1 = \frac{EC}{AE} + 1$ $\frac{DB+AD}{AD}=\frac{EC+AE}{AE}$$\frac{AB}{AD}=\frac{AC}{AE}$$\frac{6}{2}=\frac{9}{AE}$$AE=\frac{9}{3}$$AE=3 cm$$AE$ 的长度为 $3 cm$。
"\已知：在 $Δ\ ABC$ 中，$D$ 和 $E$ 分别是边 $AB$ 和 $AC$ 上的点，使得 $DE\ ||\ BC$。$AD\ =\ 4\ cm$，$AE\ =\ 8\ cm$，$DB\ =\ x\ –\ 4\ cm$ 且 $EC\ =\ 3x\ –\ 19$。求解：我们需要求 $x$ 的值。解：$DE\ ||\ BC$（已知）根据基本比例定理，$\frac{AD}{DB}\ =\ \frac{AE}{EC}$$ \begin{array}{l}\frac{4}{x-4} =\frac{8}{3x-19}\\\\4( 3x-19) =8( x-4)\\\\3x-19=2( x-4)\\\\3x-19=2x-8\\\\3x-2x=19-8\\\\x=11\ cm\end{array}$$x$ 的值为 $11 cm$。
已知：在 $Δ\ ABC$ 中，$D$ 和 $E$ 分别是边 $AB$ 和 $AC$ 上的点，使得 $DE\ ||\ BC$。$AD\ =\ 8\ cm$，$AB\ =\ 12\ cm$ 且 $AE\ =\ 12\ cm$。求解：我们需要求 $CE$ 的长度。解：$DE\ ||\ BC$（已知）$AB=AD+DB$$DB=AB-AD=(12-8) cm$$DB=4 cm$根据基本比例定理，$ \begin{array}{l}\frac{AD}{DB} =\frac{AE}{EC}\\\\\frac{8}{4} =\frac{12}{EC}\\\\EC=\frac{12\times 4}{8}\\\\EC=6\ cm\end{array}$$CE$ 的长度为 $6 cm$。
已知：给定的数字是 23。求解：我们需要画出 23 的因数树。解：23 是一个质数。因此，23 的因数是 1 和 23。
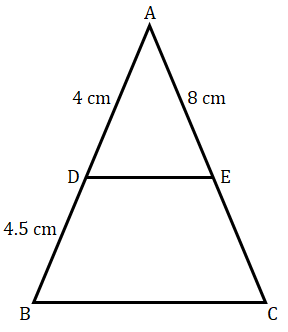
"\已知：在 $Δ$ ABC 中，D 和 E 分别是边 AB 和 AC 上的点，使得 DE $||$ BC。AD = 4 cm，DB = 4.5 cm，AE = 8 cm。求解：我们需要求 AC 的值。解：DE $||$ BC（已知）根据基本比例定理， $\frac{AD}{DB}=\frac{AE}{EC}$$\frac{4}{4.5} =\frac{8}{EC}$$EC=\frac{8\times 4.5}{4}$$EC=\frac{36}{4}$$EC=9 cm$从图中可以看出，$AC=AE+EC$$AC=(8+9) cm$$AC=17 cm$$AC$ 的长度为 $17 cm$。
"\已知：在 $Δ\ ABC$ 中，$D$ 和 $E$ 分别是边 $AB$ 和 $AC$ 上的点，使得 $DE\ ||\ BC$。$\frac{AD}{DB}\ =\ \frac{2}{3}$ 且 $AC\ =\ 18\ cm$。求解：我们需要求 $AE$ 的长度。解：$DE\ ||\ BC$（已知）根据基本比例定理， $\frac{AD}{DB}\ =\ \frac{AE}{EC}$两边都加 1， $\frac{AD}{DB} + 1 = \frac{AE}{EC} + 1$$\frac{2}{3} + 1 =\frac{AE+EC}{EC}$ ($\frac{AD}{DB}\ =\ \frac{2}{3}$)$\frac{2+3}{3} =\frac{AC}{EC}$ ($AE+EC=AC$)$\frac{5}{3} =\frac{18}{EC}$$EC= \frac{18\times3}{5}$$EC=\frac{54}{5} cm$$AE=AC-EC$$AE=18-\frac{54}{5} cm$$AE=\frac{18\times5-54}{5}$$AE=\frac{90-54}{5}$$AE=\frac{36}{5} cm$$AE=7.2 cm$$AC$ 的长度为 $7.2 cm$。 阅读更多