数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
已知：在连接点 $P\ ( a, \ b)$ 和 $Q\ ( b, \ a)$ 的线段上有一个点 $R\ ( x, \ y)$ 。需要证明：$a+b=x+y$。解答：$\because \ R( x, \ y)$ 在线段上，连接点 $P( a, \ b)$ 和 $Q( b, \ a)$ ，$R( x, \ y) ,\ P( a, \ b) \ 和\ Q( b, \ a)$ 共线。三角形 $\vartriangle PQR\ $ 的面积 A 应该为 0。我们知道，顶点为 $( x_{1} ,\ y_{1}) ... 阅读更多
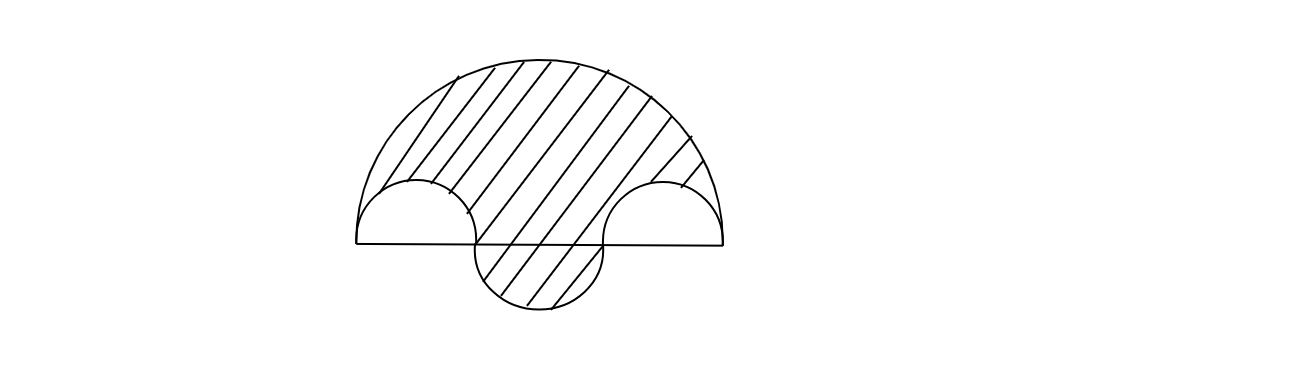
"\已知：由四个半圆弧组成的边界区域。最大弧的直径为 $14\ cm$，最小弧的直径为 $3.5\ cm$。需要求解：阴影区域的面积。解答：已知最大半圆的直径 $AB=14\ cm$，最小半圆的直径 $AC=DB=3.5\ cm$，中间半圆的直径 $CD=AB-( AC+BD)$ $=14-( 3.5+3.5)$ $=7\ cm$。最大半圆的面积 $A_{1} =\frac{\pi }{2}\left(\frac{AB}{2}\right)^{2}$ $=\frac{1}{2} \times \frac{22}{7} \times \left(\frac{14}{2}\right)^{2}$ $=77\ cm^{2}$。中间半圆的面积... 阅读更多
已知：8、9 和 25。需要求解：应用质因数分解法求出给定整数的 LCM 和 HCF。解答：使用质因数分解法计算 LCM 和 HCF：将数字写成其质因数的乘积：8 的质因数分解：$2\ \times\ 2\ \times\ 2\ =\ 2^3$；9 的质因数分解：$3\ \times\ 3\ =\ 3^2$；25 的质因数分解：$5\ \times\ 5\ =\ 5^2$。将每个质数的最高次幂相乘：$2^3\ \times\ 3^2\ \times\ 5^2\ =\ 1800$。LCM(8, 9, 25) = 1800。将所有公有的质因数相乘：没有公有的质因数。所以，HCF(8, 9, 25) = 1。因此，8、9 和 25 的 LCM 和 HCF 分别为 1800 和 1。
已知：40、36 和 126。需要求解：应用质因数分解法求出给定整数的 LCM 和 HCF。解答：使用质因数分解法计算 LCM 和 HCF：将数字写成其质因数的乘积：40 的质因数分解：$2\ \times\ 2\ \times\ 2\ \times\ 5\ =\ 2^3\ \times\ 5^1$；36 的质因数分解：$2\ \times\ 2\ \times\ 3\ \times\ 3 =\ 2^2\ \times\ 3^2$；126 的质因数分解：$2\ \times\ 3\ \times\ 3\ \times\ 7\ =\ 2^1\ \times\ 3^2\ \times\ 7^1$。将每个质数的最高次幂相乘：$2^3\ \times\ 3^2\ \times\ 5^1\ \times\ 7^1\ =\ 2520$。LCM(40, 36, 126) = 2520。将所有公有的质因数相乘：$2^1\ =\ 2$。HCF(40, 36, 126) = 2。因此，40、36 和 126 的 LCM 和 HCF 分别为 2520 和 2。
已知：84、90 和 120。需要求解：应用质因数分解法求出给定整数的 LCM 和 HCF。解答：使用质因数分解法计算 LCM 和 HCF：将数字写成其质因数的乘积：84 的质因数分解：$2\ \times\ 2\ \times\ 3\ \times\ 7\ =\ 2^2\ \times\ 3^1\ \times\ 7^1$；90 的质因数分解：$2\ \times\ 3\ \times\ 3\ \times\ 5\ =\ 2^1\ \times\ 3^2\ \times\ 5^1$；120 的质因数分解：$2\ \times\ 2\ \times\ 2\ \times\ 3\ \times\ 5\ =\ 2^3\ \times\ 3^1\ \times\ 5^1$。将每个质数的最高次幂相乘：$2^3\ \times\ 3^2\ \times\ 5^1\ \times\ 7^1\ =\ 2520$。LCM(84, 90, 120) = 2520。将所有公有的质因数相乘：$2^1\ \times\ 3^1\ =\ 6$。HCF(84, 90, 120) = 6。因此，84、90 和 120 的 LCM 和 HCF 分别为 2520 和 6。
已知：24、15 和 36。需要求解：应用质因数分解法求出给定整数的 LCM 和 HCF。解答：使用质因数分解法计算 LCM 和 HCF：将数字写成其质因数的乘积：24 的质因数分解：$2\ \times\ 2\ \times\ 2\ \times\ 3\ =\ 2^3\ \times\ 3^1$；15 的质因数分解：$3\ \times\ 5\ =\ 3^1\ \times\ 5^1$；36 的质因数分解：$2\ \times\ 2\ \times\ 3\ \times\ 3\ =\ 2^2\ \times\ 3^2$。将每个质数的最高次幂相乘：$2^3\ \times\ 3^2\ \times\ 5^1\ =\ 360$。LCM(24, 15, 36) = 360。将所有公有的质因数相乘：$3^1\ =\ 3$。HCF(24, 15, 36) = 3。因此，24、15 和 36 的 LCM 和 HCF 分别为 360 和 3。
已知：306 和 657 的 HCF 为 9。需要求解：求出给定整数对的 LCM。解答：我们知道：LCM $\times$ HCF = 两个整数的乘积。现在，LCM $\times$ 9 = 306 $\times$ 657；LCM $\times$ 9 = 201042；LCM = $\frac{201042}{9}$；LCM = 22338。因此，306 和 657 的 LCM 为 22338。
已知：HCF = 16；LCM = 380。需要解答：检查两个数是否可以有 16 作为它们的 HCF 和 380 作为它们的 LCM。解答：HCF 是两个数的最大公约数，LCM 是这两个数的最小公倍数。因此，对于一对数，LCM 必须能被这两个数的 HCF 整除。因此，如果两个数的 HCF 为 16，LCM 为 380，那么 380 必须能被 16 整除。现在，$\frac{380}{16}\ =\ 23.75$。我们可以看到 380 不能被 16 整除。因此，两个数不可能有 16 ... 阅读更多
已知：两个数的最大公约数（HCF）是 145，最小公倍数（LCM）是 2175。其中一个数是 725。求：已知最大公约数和最小公倍数，求另一个数。解：设所求的数为 a。我们知道：LCM × HCF = 两个整数的乘积因此，2175 × 145 = 725 × a315375 = 725aa = 315375 ÷ 725a = 435所以，所求的数是 435。