数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学
已知：一个等差数列，首项 a=2，末项 l=29，各项之和 S=155。求：求该等差数列的公差。解：在给定的等差数列中，首项 a=2，末项 l=29，公差 d=?，项数 n=?。已知等差数列 n 项和 = n/2(a+l)，代入 a, l 和和的值，得到 155 = n/2(2+29)，=> 31n=310，=> n=310/31 =10。这里我们得到项数 n=10。等差数列的第 n 项 = a+(n-1)d，=> 29=2+(10-1)d … 阅读更多
已知：一个平行四边形，其所有边都与一个圆相切。求证：该平行四边形是菱形。证明：我们画一个外切于圆的平行四边形 PQRS，其所有边都与圆相切于点 A、B、C 和 D。由于它是一个平行四边形，所以 PS=QR 和 PQ=RS。我们知道，从同一点引出的圆的切线长度总是相等的。PB=PA，QD=QA，RD=RC，SC=SB。将以上四个等式相加，(PB+QD+RD+SC)=(PA+QA+RC+SB)，(QD+RD)+(PB+SC)=(PA+QA)+(RC+SB)，QR+(PB+SB)=PQ+(RC+SC) … 阅读更多
已知：平行四边形 ABCD，顶点为 A(1, 2)、B(4, 3) 和 C(6, 6)。求：求第四个顶点 D 的坐标。解：这里 ABCD 是一个平行四边形，AC 和 BD 是它的对角线，它们互相平分，相交于点 O。点 O 是 AC 和 BD 的中点。如果 O 是 AC 的中点，=> O=( (1+6)/2 , (2+6)/2 )，因此 O=(7/2, 4)。O 也是 BD 的中点。设 D 点坐标为 (x, y)，因此 O=((x+4)/2, (y+3)/2)。但我们知道 O=(7/2, 4)，因此 (7/2, 4)=((x+4)/2, (y+3)/2)，=> (x+4)/2 = 7/2 并且 … 阅读更多
已知：3x=cscθ 且 3/x=cotθ。求：求 3(x² - 1/x²) 的值。解：已知 3x=cscθ 且 3/x=cotθ，则 (3x)² - (3/x)² = csc²θ - cot²θ，=> 9x² - 9/x² = 1 (因为 csc²θ - cot²θ = 1)，=> 9(x² - 1/x²) = 1，=> 3(x² - 1/x²) = 1/3。因此，3(x² - 1/x²) 的值为 1/3。
已知：连接两点 A(6,-5) 和 B(-2,11) 的线段，点 P(2, p) 是该线段的中点。求：求 p 的值。解：如果有一条线段连接两点 A(x₁, y₁) 和 B(x₂, y₂)，则中点 p(x, y) 为 (x, y) =((x₁+x₂)/2, (y₁+y₂)/2)，因此 (2, p) =((6-2)/2, (-5+11)/2)，=> (2, p) =(4/2, 6/2)，=> (2, p) =(2, 3)，因此 p=3。
已知：a) 本金 = 1200 卢比，年利率为 12% b) 本金 = 7500 卢比，年利率为 5%。求：求每种情况下 3 年末应支付的金额。解：a) 这里，本金 P = 1200 卢比，利率 R=12%/年，时间 T=3 年。单利 = (P × R × T)/100 = (1200 × 12 × 3)/100 = 432 卢比。现在，金额 = 本金 + 单利 = 1200 卢比 + 432 卢比 = 1632 卢比。b) 这里，本金 P=7500 卢比，利率 R=5%/年，时间 T=3 年。单利 = (P × R × T)/100 = (7500 × 5 × 3)/100 = 1125 卢比。现在，金额 = 本金 + 单利 = 7500 卢比 + 1125 卢比 = 8625 卢比。三年后应支付的金额为：a) 1632 卢比 b) 8625 卢比
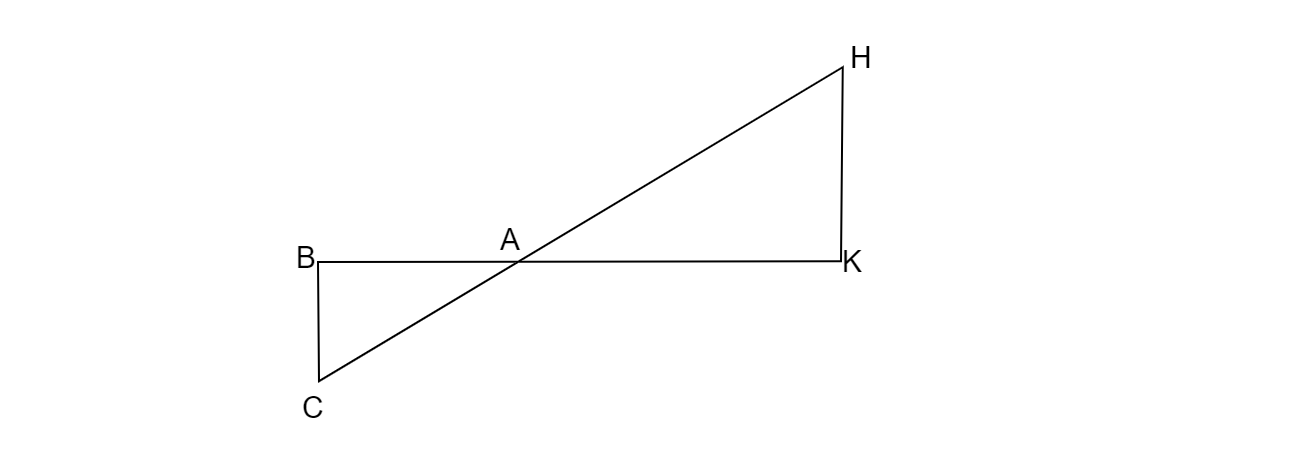
。如果 AK=10 厘米已知：在图 2 中，△AHK～△ABC，AK=10 厘米，BC=3.5 厘米。求：求 AC。解：已知 △AHK～△ABC，=> AH/AB = HK/BC = AK/AC，=> HK/BC = AK/AC。代入 AK=10 厘米，BC=3.5 厘米和 HK=7 厘米，=> 7/3.5 = 10/AC，=> AC=(10×3.5)/7，=> AC=5 厘米。
已知：浴室长度 = 500 厘米，浴室宽度 = 350 厘米，正方形瓷砖边长 = 25 厘米，瓷砖价格 = 60 卢比/块。求：求瓷砖的总价。解：我们知道，长方形面积 = 长 × 宽，正方形面积 = 边长 × 边长。浴室面积 = 500 × 350，瓷砖面积 = 25 × 25。所需的瓷砖数量 = 浴室面积 / 正方形瓷砖面积 = 500 … 阅读更多
已知：给定的数字是 10500 和 16800。求：求给定数字的最大公约数 (HCF)。解：10500 和 16800。10500 可以写成 105 × 100，16800 可以写成 168 × 100。因此，100 是 10500 和 16800 的公因数。现在，我们可以找到 105 和 168 的公因数，并乘以 100。105 的质因数 = 3 × 5 × 7，168 的质因数 = 2 × 2 × 2 × 3 × 7。公因数是 3 × 7 = 21。HCF = 21 × 100 = 2100。因此，10500 和 16800 的最大公约数 (HCF) 是 2100。
已知：已知项为：（i） $3^2 \times (-4)^2 = (-12)^{2x}$ （ii） $(\frac{9}{4})^{3} \times (\frac{8}{9})^{3}=2^{6 x}$。 求解：我们需要求出已知项中的x值。 解：（i） $3^2 \times (-4)^2 = (-12)^{2x}$ 我们知道，$a^m \times b^m = (a.b)^m$ 所以， $3^2 \times (-4)^2 = (3 \times (-4))^2$ $\Rightarrow (3 \times (-4))^2 = (-12)^{2x}$ $\Rightarrow (-12)^2 = (-12)^{2x}$ 由于底数相等，我们可以得出，$2 = 2x$ 改写为，$2x = 2$ $x = \frac{2}{2} = 1$ 因此，x的值为1。（ii） $(\frac{9}{4})^{3} \times (\frac{8}{9})^{3}=2^{6 x}$ 我们知道，$a^m \times b^m = (a.b)^m$ 所以，$(\frac{9}{4})^{3} \times (\frac{8}{9})^{3}=(\frac{9}{4} \times \frac{8}{9})^{3}$ $\Rightarrow (\frac{9}{4} \times \frac{8}{9})^{3} = 2^{6 x}$ $\Rightarrow (2)^3 ... 阅读更多