已知:以 O 为圆心的两个同心圆及其从外点 P 引出的切线 AP 和 BP。AP = 15 厘米。求解:求 BP 的值。解:连接 OP。因为圆的切线总是垂直于半径,所以∠A = ∠B = 90°。在直角三角形△OAP 中,根据勾股定理,OP² = OA² + AP² = 8² + 15² = 64 + 225 = 289,所以 OP = √289 = 17 厘米。在直角三角形△OBP 中,根据勾股定理,OB² + BP² = OP²,所以 5² + BP² = 17²,BP² + 25 = 289,BP² = 289 - 25 = 264,BP = √(2 × 2 × 66) = 2√66 厘米。因此,BP 的长度为 2√66 厘米。阅读更多
已知:方程 x + 3y = 6; 2x - 3y = 12。求解:用图形方法解方程。解:给定的方程为:x + 3y = 6 ....................(1) 2x - 3y = 12 ....................(2)在方程 (1) 中,x + 3y = 6,x = 6 - 3y。方程 (1) 的不同 y 值对应的表格。x|6|3|0 y|0|1|2在方程 (2) 中,2x - 3y = 12,2x = 12 + 3y,x = (12 + 3y) / 2。方程 (2) 的不同 y 值对应的表格。x|0|6|3 y|-4|0|-2通过在图上绘制点 A(6, 0), B(3, 1), C(0, 2), D(3, -2) 和 E(0, -4),我们发现两条直线相交于 A(6, 0)。因此,x = 6,y = 0。
已知:点 A(0, 2) 与点 B(3, p) 和 C(p, 5) 等距。求解:求 p 的值。解:因为 A(0, 2) 与点 B(3, p) 和 C(p, 5) 等距,所以 AB = AC,AB² = AC²。已知两点 (x₁, y₁) 和 (x₂, y₂) 之间的距离 = √[(x₂ - x₁)² + (y₂ - y₁)²]。使用距离公式,AB = √[(3 - 0)² + (p - 2)²] = √[3² + p² + 4 - 4p] = √[p² - 4p + 13],AB² = p² - 4p + 13。类似地,AC = √[(p - 0)² + (5 - 2)²] = √[p² + 3²] = √[p² + 9],AC² = p² + 9。因为 AB² = AC²,所以 p² - 4p + 13 = p² + 9,...阅读更多
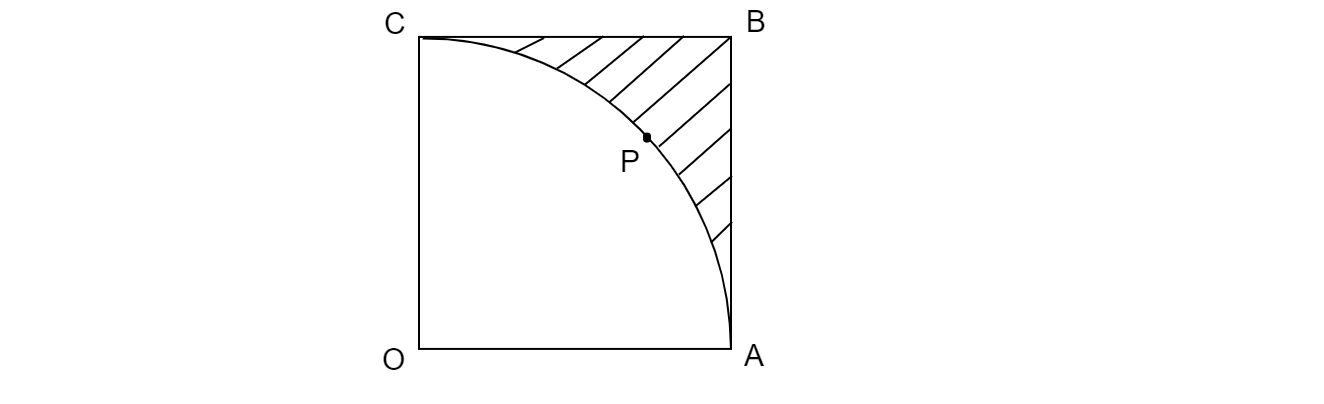
已知:正方形 OABC 的边长 = 7 厘米。以 O 为圆心的四分之一圆 OAPC。求解:求阴影部分的面积。解:OA 为给定正方形的边长,所以 OA = 7 厘米。正方形 OABC 的面积 = (边长)² = 7² = 49 平方厘米。OA 是四分之一圆 OAPC 的半径,r = 7 厘米。四分之一圆 OAPC 的面积 = (1/4) × πr² = (1/4) × (22/7) × 7 × 7 = 77/2 平方厘米。阴影部分的面积 = 正方形 OABC 的面积 - 四分之一圆 OAPC 的面积 = 49 - 77/2 = 49 - 38.5 = 10.5 平方厘米。因此,阴影部分的面积为 10.5 平方厘米。阅读更多
已知:(x - √5) 是多项式 x³ - 3√5x² - 5x + 15√5 的一个因式。求解:求该多项式的所有零点。解:设 P(x) = x³ - 3√5x² - 5x + 15√5。因为 (x - √5) 是该多项式的一个因式,所以我们代入 x = √5:P(√5) = (√5)³ - 3√5(√5)² - 5(√5) + 15√5 = 5√5 - 15√5 - 5√5 + 15√5 = 0。所以 (x - √5) 是 P(x) 的一个因式。因此,(x + √5)(x - √5) = x² - 5 是 P(x) 的一个因式。用 x² - 5 除以给定的多项式,所以 x - 3√5 是该多项式的因式。所以 x - 3√5 = 0,x = 3√5。所以 √5,-√5,…阅读更多
已知:506 和 1155。求解:这里我们要找到给定整数对的最大公约数 (HCF),并将其表示为线性组合。解:使用欧几里得除法算法求 HCF:使用欧几里得引理得到:1155 = 506 × 2 + 143 ...(i)现在,考虑除数 506 和余数 143,并应用除法引理得到:506 = 143 × 3 + 77 ...(ii)现在,考虑除数 143 和余数 77,并应用除法引理得到:143 = 77 × 1 + 66 ...(iii)现在,考虑除数 77 和余数 66,并应用除法引理得到:…阅读更多
已知:1288 和 575。求解:这里我们要找到给定整数对的最大公约数 (HCF),并将其表示为线性组合。解:使用欧几里得除法算法求 HCF:使用欧几里得引理得到:1288 = 575 × 2 + 138 ...(i)现在,考虑除数 575 和余数 138,并应用除法引理得到:575 = 138 × 4 + 23 ...(ii)现在,考虑除数 138 和余数 23,并应用除法引理得到:138 = 23 × 6 + 0 ...(iii)余数已变为零,…阅读更多
已知:408 和 1032 的最大公约数 (HCF) 可以表示为 1032m - 408 × 5。求解:这里我们要找到 m 的值。解:为了找到 m 的值,我们必须计算 408 和 1032 的最大公约数 (HCF)。使用欧几里得引理得到:1032 = 408 × 2 + 216现在,考虑除数 408 和余数 216,并应用除法引理得到:408 = 216 × 1 + 192现在,考虑除数 216 和余数 192,并应用除法引理得到:216 = 192 × 1 + 24现在,考虑除数 192 和余数…阅读更多
已知:657和963的最大公约数可以表示为 657x + 963 × (–15) 的形式。求解:我们需要求x的值。解:为了求x的值,我们必须计算657和963的最大公约数。使用欧几里得算法:963 = 657 × 1 + 306现在,考虑除数657和余数306,并应用除法定理:657 = 306 × 2 + 45现在,考虑除数306和余数45,并应用除法定理:306 = 45 × 6 + 36现在,考虑除数45和余数36,并... 阅读更多
已知:一位商人有120升一种油,180升另一种油,240升第三种油。求解:我们需要求油桶的最大容量。解:已知这位商人想把这三种油装入容量相同的油桶中出售。为了求这种油桶的最大容量,我们需要计算120、180和240的最大公约数。首先,让我们使用欧几里得算法求120和180的最大公约数:使用欧几里得算法:180 = 120 × 1 + 60现在,考虑除数120和余数60,并... 阅读更多

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP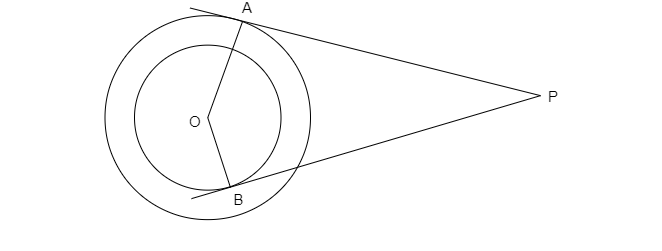 "\
"\
 "\
"\