已知 $x-\sqrt{5}$ 是多项式 $x^{3} -3\sqrt{5} x^{2} -5x+15\sqrt{5}$ 的一个因式，求该多项式的所有零点。

已知： $x-\sqrt{5}$ 是多项式 $x^{3} -3\sqrt{5} x^{2} -5x+15\sqrt{5}$ 的一个因式。

求解：求出该多项式的所有零点。

解：

设 $P(x) =x^{3} -3\sqrt{5} x^{2} -5x+15\sqrt{5}$。

因为 $x-\sqrt{5}$ 是该多项式的一个因式。

现在我们令 $x=\sqrt{5}$

$P(\sqrt{5}) = (\sqrt{5})^{3} -3\sqrt{5}(\sqrt{5})^{2} -5(\sqrt{5}) +15\sqrt{5} = 5\sqrt{5} - 15\sqrt{5} - 5\sqrt{5} + 15\sqrt{5} = 0$

因此 $(x-\sqrt{5})$ 是一个因式

$=0$

$\therefore \ (x-\sqrt{5})$ 是 $P(x)$ 的一个因式

$\therefore \ (x+\sqrt{5})(x-\sqrt{5}) =x^{2} -5$ 是 $P(x)$ 的一个因式

用 $x^{2} -5$ 除以给定的多项式。

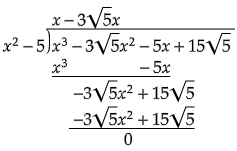
$\therefore \ x-3\sqrt{5}$ 是该多项式的因式。

$\therefore \ x-3\sqrt{5} =0$

$\Rightarrow x=3\sqrt{5}$

$\therefore \sqrt{5} ,\ -\sqrt{5}$ 和 $3\sqrt{5}$ 是该多项式的零点。

Tutorialspoint

更新于： 2022年10月10日

62 次浏览

开启你的职业生涯

完成课程获得认证

开始学习